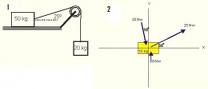
Leyes de Newton
| ||||||
Leyes de Newton, también conocidas como Leyes del movimiento de Newton o Leyes de la Dinámica, son tres principios a partir de los cuales se explican la mayor parte de los problemas planteados por la dinámica, en particular aquel relativos al movimiento de los cuerpos o sea se explicaba el movimiento de los cuerpos así como sus efectos y causas. Las Leyes de Newton permiten explicar tanto el movimiento de los astros como los movimientos de los proyectiles artificiales creados por el ser humano, así como toda la mecánica de funcionamiento de las máquinas.
Sumario
Historia
La formulación matemática fue publicada por Isaac Newton en 1687, en su obra Philosophiae Naturalis Principia Mathematica. Las leyes de Newton constituyen, junto con la transformación de Galileo, la base de la mecánica clásica. En el tercer volumen de los Principia Newton mostró que, combinando estas leyes con su Ley de la gravitación universal, se pueden deducir y explicar las Leyes de Kepler sobre el movimiento planetario.
Fundamentos teóricos de las leyes
Newton planteó que todos los movimientos se atienen a tres leyes principales formuladas en términos matemáticos y que implican conceptos que es necesario primero definir con rigor. El primer concepto que maneja Newton es el de masa, que identifica con "cantidad de materia" otro concepto es la fuerza, causa del movimiento; los dos son denominados habitualmente por las letras F y m.
Fuerza
- Causa del movimiento (F).
Masa
- Medición de la cantidad de materia puesta en movimiento (m).
Newton asume a continuación que la cantidad de movimiento es el resultado del producto de la masa por la velocidad. En tercer lugar, precisa la importancia de distinguir entre lo absoluto y relativo siempre que se hable de tiempo, espacio, lugar o movimiento.
En este sentido, Newton, que entiende el movimiento como una traslación de un cuerpo de un lugar a otro, para llegar al movimiento absoluto y verdadero de un cuerpo compone el movimiento (relativo) de ese cuerpo en el lugar (relativo) en que se lo considera, con el movimiento (relativo) del lugar mismo en otro lugar en el que esté situado, y así sucesivamente, paso a paso, hasta llegar a un lugar inmóvil, es decir, al sistema de referencias de los movimientos absolutos.
De acuerdo con esto, Newton establece que los movimientos aparentes son las diferencias de los movimientos verdaderos y que las fuerzas son causas y efectos de estos. Consecuentemente, la fuerza en Newton tiene un carácter absoluto, no relativo.
Las leyes
Primera ley de Newton o ley de la inercia
Todo cuerpo continúa en su estado de reposo, o de movimiento uniforme en una línea recta, a menos que sea obligado a cambiar ese estado por fuerzas aplicadas sobre él. [1]
El movimiento es relativo, es decir, depende de cual sea el observador que describa el movimiento. Así, para un pasajero A sentado un tren, otro pasajero B también sentado esta en reposo, mientras que para alguien que ve pasar el tren desde el andén de una estación, tanto el pasajero A como el B se están moviendo a una gran velocidad. Se necesita, por tanto, un sistema de referencia al cual referir el movimiento.
La primera ley de Newton sirve para definir un tipo especial de sistemas de referencia conocidos como Sistemas de referencia inerciales, que son aquellos sistemas de referencia desde los que se observa que un cuerpo sobre el que no actúa ninguna fuerza neta se mueve con velocidad constante.
En realidad, es imposible encontrar un sistema de referencia inercial, puesto que siempre hay algún tipo de fuerzas actuando sobre los cuerpos, pero siempre es posible encontrar un sistema de referencia en el que el problema que se está estudiando se pueda tratar como si se estuviera en un sistema inercial. En muchos casos, suponer a un observador fijo en la Tierra es una buena aproximación de sistema inercial.
Ejemplo
Un buen ejemplo en el que se aprecia esta fuerza, es cuando un ómnibus se detiene de manera brusca, si las personas en el ómnibus no se encuentran sujetas continuarán su movimiento rectilíneo (se desplazarán hacia adelante), si por el contrario el ómnibus esta detenido y comienza a moverse bruscamente la tendencia será a mantener el estado de reposo (se desplazarán hacia atrás)
Segunda ley de Newton o ley de fuerza
La fuerza define la dirección en que el cuerpo se pone en movimiento o cambia dicho movimiento. Ambas, fuerza y masa, determinan la rapidez con que el cuerpo cambia su reposo o movimiento: cuanto mayor sea la fuerza aplicada y menor la masa del cuerpo, mayor será dicha rapidez.[1]
Esta ley se encarga de cuantificar el concepto de fuerza. En términos matemáticos se expresa mediante la relación:
F = m • a
Tanto la fuerza como la aceleración son magnitudes vectoriales, es decir, tienen, además de un valor, una dirección y un sentido. De esta manera, la Segunda ley de Newton debe expresarse como:
→ →
F = m • a
La unidad de fuerza en el Sistema Internacional es el Newton y se representa por N. Un Newton es la fuerza que hay que ejercer sobre un cuerpo de un kilogramo de masa para que adquiera una aceleración de 1 m/s2, o sea,
1 N = 1 Kg • 1 m/s2
La expresión de la Segunda ley de Newton que hemos dado es válida para cuerpos cuya masa sea constante. Si la masa varia, como por ejemplo un cohete que va quemando combustible, no es válida la relación F = m • a.
Vamos a generalizar la Segunda ley de Newton para que incluya el caso de sistemas en los que pueda variar la masa. Para ello primero vamos a definir una magnitud física nueva. Esta magnitud física es la cantidad de movimiento que se representa por la letra p y que se define como el producto de la masa de un cuerpo por su velocidad, es decir:
p = m • v
La cantidad de movimiento también se conoce como momento lineal. Es una magnitud vectorial y, en el Sistema Internacional se mide en Kg•m/s . En términos de esta nueva magnitud física, la Segunda ley de Newton se expresa de la siguiente manera:
La Fuerza que actúa sobre un cuerpo es igual a la variación temporal de la cantidad de movimiento de dicho cuerpo, es decir,
F = dp/dt
De esta forma incluimos también el caso de cuerpos cuya masa no sea constante
Tercera ley de Newton o ley de acción y reacción
Si un cuerpo A ejerce una fuerza sobre otro B, entonces, el cuerpo B ejercerá una fuerza sobre el A, de igual valor; pero en sentido contrario. [1]
Matemáticamente la tercera ley del movimiento de Newton suele expresarse como sigue:
F1 = F2'
donde F1 es la fuerza que actúa sobre el cuerpo 1 y F2' es la fuerza reactiva que actúa sobre el cuerpo 2
Ejemplo
Cuando en una piscina un bañista A empuja a otro bañista B, ambos se desplazan en sentido contrario aunque este último no haga el intento de empujar al primero. Esto se debe a la reacción que el bañista B hace sobre el bañista A.
Es importante observar que este principio de acción y reacción relaciona dos fuerzas que no están aplicadas al mismo cuerpo, produciendo en ellos aceleraciones diferentes, según sean sus masas. Por lo demás, cada una de esas fuerzas obedece por separado a la segunda ley es decir aunque los pares de acción y reacción tenga el mismo valor y sentidos contrarios, no se anulan entre si, puesto que actúan sobre cuerpos distintos.
Límites de validez de las leyes de Newton
Las leyes que constituyen las bases de la dinámica, se conocen bajo el nombre de leyes del movimiento mecánico y fueron formuladas en 1687 por Isaac Newton, estas leyes permitieron comprender el comportamiento de los fenómenos mecánicos y dar explicación a otros como el movimiento de la Tierra alrededor del Sol, el movimiento de los péndulos, de cuerpos suspendidos por muelles como determinar con exactitud el movimiento de los vehículos espaciales e incluso predecir su comportamiento, pero estas leyes tienen límite en su validez.
La primera Ley de Newton o ley de la inercia
Esta primera ley solo se cumple para un Sistema Inercial y una partícula- punto material, para entender dicho planteamiento se debe conocer que para estudiar el movimiento de un cuerpo, se analiza primero un sistema de referencia. Un mismo movimiento parece diferente si se observa desde distintos sistemas de referencia. Un sistema se define como inercial si está en reposo o en Movimiento Rectilíneo Uniforme. Punto material, es la idealización de un cuerpo al que suponemos con masa pero sin ocupar volumen lo que supone asignarle una densidad infinita (d= m/v ).
La segunda ley de Newton o ley de fuerza
Esta ley sólo se cumple en Sistemas Inerciales. (En Sistemas no Inerciales la fórmula válida es: F +Fi = m•a), para masas no muy pequeñas (que no tengan implicaciones cuánticas) y para velocidades pequeñas v <<< c (velocidad de la luz). Según la Dinámica clásica una fuerza actuando sobre un cuerpo le comunica una aceleración a= cte, pero la velocidad crece indefinidamente v = a•t . Si esto fuera así en un tiempo infinito la velocidad sería infinita, lo cual está en desacuerdo con la experiencia y está explicado en la mecánica relativista que le pone un límite a V= 3•10 8 m/s.
La tercera ley de Newton o ley de acción y reacción
Las fuerzas proceden de una interacción y siempre aparecen de dos en dos. Se aplica cada una en uno de los cuerpos que interaccionan, (sí se aplicaran las dos en el mismo cuerpo producirían reposo). Para obtener equilibrio se requiere dos o más interacciones sobre un cuerpo para que las fuerzas originadas se anulen.
Sólo se cumple la tercera Ley si el tiempo de interacción es suficientemente largo para que se establezca la respuesta a la acción.
Al resolver los problemas de dinámica, se aplican las leyes de Newton sin pensar si ellas son válidas en todos los casos, tampoco se tiene en cuenta si el sistema de referencia en que se analiza el movimiento de los cuerpos puede influir al operar con dichas leyes, o si los valores de las velocidades a que se mueven los cuerpos, pueden limitar la aplicación de ellas, incluso se habla de cuerpos que son considerados como punto material, que como resultado de las interacciones solo experimentan variaciones en su movimiento de traslación.
Ver además
Referencias
Fuentes
- Dr. Pablo Valdés, Castro (2009). Física Octavo Grado. La Habana: Editorial Pueblo y Educación.
- Isaac Newton - Leyes del movimiento de Newton .
- La Dinámica de Newton .
- Leyes del movimiento, de Newton .
- Leyes de Newton.
- Leyes de Newton - Wikipedia .
- Física/Dinámica/Leyes de Newton - Wikilibros .
Bibliografía
- Núñez Viera y col. Física 10 Grado. Editorial Félix Varela. 2003
- Portuondo Duany R. Pérez Quintana. Mecánica. Editorial Pueblo y Educación. 1983