Leyes de Kepler
| ||||||
Leyes de Kepler. Enunciadas por Johannes Kepler para describir matemáticamente el movimiento de los planetas en sus órbitas alrededor del Sol.
Sumario
Historia
En el siglo XVI, el astrónomo polaco Nicolás Copérnico remplazó la tradición de la tierra como centro del movimiento planetario con uno en el cual el sol es el centro y los planetas se mueven alrededor en círculos y los astrónomos comenzaron a aceptar la idea de que la Tierra y los planetas giraban alrededor del Sol, en lugar de que el Sol y los planetas giraran alrededor de la Tierra.
A través del modelo de Copérnico llegó a ser cercana la predicción correcta del movimiento de los planetas. Esto llega a ser particularmente evidente en el caso del planeta Marte, cuya órbita fue medida muy exactamente por el astrónomo danés Tycho Brahe, sin embargo los astrónomos no eran capaces aún de describir el movimiento de los planetas con precisión.
El astrónomo alemán Johannes Kepler fue quien finalmente tuvo la capacidad de describir el movimiento planetario utilizando tres expresiones matemáticas, las cuales llegaron a ser conocidas como las leyes de movimiento planetario de Kepler, quien además encontró que las órbitas planetarias no eran circulares, sino elípticas. Las tres leyes referentes al movimiento de los planetas en sus órbitas alrededor del Sol, descubiertas por Kepler, no solo se aplican a los planetas que orbitan alrededor del Sol, sino todos los casos de cuerpos celestes que orbitan bajo la influencia de la gravedad.
Leyes de Kepler
- Primera ley de Kepler (órbitas elípticas)
Los planetas describen órbitas elípticas estando el Sol en uno de sus focos.
La elipse se ve como un círculo alargado: un eje largo, llamado eje mayor; perpendicular a el eje mayor está el eje menor el más corto. Los 2 focos están simétricamente localizados en cada lado del eje mayor.
- Segunda ley de Kepler
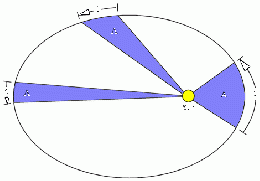
Los cuerpos celestes describen trayectorias en las que se cumple que: las áreas barridas por el radio vector en tiempos iguales son iguales. El radio vector va desde el foco de la elipse a la posición del planeta en cada instante.
La ley de las áreas es equivalente a la constancia del momento angular, es decir, cuando el planeta está más alejado del Sol (afelio) su velocidad es menor que cuando está más cercano al Sol (perihelio).
- Tercera ley de Kepler
Los cuadrados de los periodos de revolución son proporcionales a los cubos de la distancia promedio al Sol.
Es decir el cuadrado del periodo del planeta es proporcional al cubo de la distancia promedio de la órbita del planeta.
A partir de la tercera ley, puede calcularse la distancia de un planeta al Sol una vez que se conoce su período.
Ley de la Gravitación Universal
Permite explicar las leyes de Kepler sobre las órbitas planetarias:
Para un planeta de masa m a una distancia r del Sol, la atracción gravitatoria será la que obliga al planeta a describir su órbita, por lo que ha de ser la fuerza centrípeta que actúa sobre el planeta. Igualando ambas fuerzas, la masa del planeta puede simplificarse y se puede obtener el cuadrado de la velocidad angular del planeta, lo que indica que cuanto mayor sea la distancia al Sol (r), menor será la velocidad del planeta. La velocidad angular del planeta se puede escribir en función del periodo de su órbita. Si se realiza el cuadrado, se agrupa periodo y radio en un miembro de la ecuación lo que aparece en el segundo miembro de la igualdad es una constante, que es justamente la tercera ley de Kepler.
Descubrimiento de la ley de la gravitación
Un momento culminante en la historia de la Física fue el descubrimiento realizado por Isaac Newton de la Ley de la Gravitación Universal: todos los objetos se atraen unos a otros con una fuerza directamente proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que separa sus centros. Al someter a una sola ley matemática los fenómenos físicos más importantes del universo observable, Newton demostró que la física terrestre y la física celeste son una misma cosa. El concepto de gravitación lograba de un solo golpe:
- Revelar el significado físico de las tres leyes de Kepler sobre el movimiento planetario.
- Resolver el intrincado problema del origen de las mareas
- Dar cuenta de la curiosa e inexplicable observación de Galileo Galilei de que el movimiento de un objeto en caída libre es independiente de su peso.
La naturaleza cuadrático inversa de la fuerza centrípetra para el caso de órbitas circulares, puede deducirse fácilmente de la tercera ley de Kepler sobre el movimiento planetario y de la dinámica del movimiento circular uniforme:
- Según la tercera ley de Kepler el cuadrado del periodo P es proporcional al cubo del semieje mayor de la elipse, que en el caso de la circunferencia es su propio radio r, P2=kr3.
- La dinámica del movimiento circular uniforme, nos dice que en una trayectoria circular, la fuerza que hay que aplicar al cuerpo es igual al producto de su masa por la aceleración normal, F=mv2/r.
- El tiempo que tarda un planeta en dar una vuelta completa es el cociente entre la longitud de la circunferencia y la velocidad, P=2π r/v.
Combinando estas expresiones, Se obtiene
F=mv2/r=m[2πr/P]21/r=4π2m[r3/P2]1/r2=4π2mk1/r2
Vemos que la fuerza F que actúa sobre el planeta en movimiento circular uniforme es inversamente proporcional al cuadrado de la distancia r desde el centro de fuerzas al centro del planeta.
Newton comparó la aceleración centrípeta de la Luna con la aceleración de la gravedad g=9.8 m/s2. La aceleración centrípeta de la Luna es ac=v2/r=4π2r/P2, con r=3.84•108 m y P=28 días=2.36•106s, se obtiene ac=2.72•10-3 m/s2. Por consiguiente,
g/ac=3602≈(60)2
Como el radio de la Tierra es 6.37•106m, y el radio de la órbita de la Luna es 3.84•108m, tenemos que
[r/R]2=[384/6.37]≈(60)2
Por tanto,
[g/ac]=[r/R]2
Las aceleraciones de ambos cuerpos están en razón inversa del cuadrado de las distancias medidas desde el centro de la Tierra.
Descripción
En la física anterior a Newton una manzana cae verticalmente hacia la Tierra en una trayectoria rectilínea, mientras que la Luna describe una órbita casi circular, que es una trayectoria cerrada.¿Cómo estas dos categorías de movimientos pueden estar relacionadas?. Si la manzana que caía verticalmente es empujada por la fuerza del aire, su trayectoria ya no será rectilínea sino el arco de una curva. Por ejemplo un proyectil disparado desde un cañón describe una trayectoria parabólica tal como se observaba en el siglo XVII en el que vivió Newton .
El salto conceptual que llevó a cabo Newton fue el de imaginar que los proyectiles podrían ser disparados desde lo alto de una montaña describiendo trayectorias elípticas (siendo la parábola una aproximación de la elipse).
Por tanto, la manzana y la Luna están cayendo, la diferencia es que la Luna tiene un movimiento de caída permanente, mientras que la manzana choca con la superficie de la Tierra.
Una misma causa produce, por tanto, los movimientos de los cuerpos celestes y terrestres.
Si se considera los movimientos de los proyectiles se puede entender fácilmente que los planetas pueden ser retenidos en ciertas órbitas mediante fuerzas centrípetas; pues una piedra proyectada se va apartando de su senda rectilínea por la presión de su propio peso y obligada a describir en el aire una curva, cuando en virtud de la sola proyección inicial habría debido continuar dicha senda recta, en vez de ser finalmente atraída al suelo; y cuanto mayor es la velocidad con la cual resulta ser proyectada más lejos llega, antes de caer a tierra. Por lo tanto, se puede suponer que la velocidad se incrementa hasta que la piedra describa un arco de 1, 2, 5, 10, 100, 1000 millas antes de caer, de forma que al final, superando los límites de la Tierra, pasará al espacio sin tocarla...
En la figura, se representa las curvas que un cuerpo describiría si fuese proyectado en dirección horizontal desde la cima de una alta montaña a más y más velocidad. Puesto que los movimientos celestes no son prácticamente retardados por la pequeña o nula resistencia de los espacios donde tienen lugar, suponga que, para conservar la analogía de los casos, que en la Tierra no hubiera aire, o al menos que éste está dotado de un poder de resistencia nulo o muy pequeño.
Entonces, por la misma razón que un cuerpo proyectado con menos velocidad describe el arco menor y, proyectado con más velocidad, un arco mayor, al aumentar la velocidad, terminará por llegar bastante más allá de la circunferencia de la Tierra, retornando a la montaña desde la que fue proyectada.
Y puesto que las áreas descritas por el movimiento del radio trazado desde el centro de la Tierra son proporcionales a su tiempo de descripción, su velocidad al retornar a la montaña no será menor que al principio, por lo que reteniendo la misma velocidad, describirá la misma curva una y otra vez, obedeciendo a la misma ley.
Fuentes
- sociedadelainformacion.com
- sc.ehu.es
- Hernández M.. Fuerza y Movimiento. Revista Española de Física, Vol 10, nº 2, 1996, págs. 44-51.