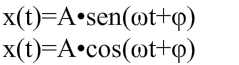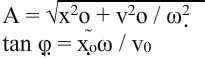Movimiento armónico simple
| ||||||
El movimiento armónico simple, también denominado movimiento vibratorio armónico simple es un movimiento rectilíneo con aceleración variable producido por las fuerzas que se originan cuando un cuerpo se separa de su posición de equilibrio, ejemplo el péndulo de un reloj o una masa suspendida de un resorte.
Un cuerpo oscila cuando se mueve periódicamente respecto a su posición de equilibrio. El movimiento armónico simple es el más importante de los movimientos oscilatorios, pues constituye una buena aproximación a muchas de las oscilaciones que se dan en la naturaleza y es muy sencillo de describir matemáticamente. Se llama armónico porque la ecuación que lo define es función del seno o del coseno.
Sumario
Movimiento armónico simple en una dirección
En el caso de que la trayectoria sea rectilínea, la partícula que realiza un m.a.s se mueve a lo largo del eje X, estando su posición x dada en función del tiempo t por las ecuaciones.
donde
- A es la amplitud o elongación máxima.
- ω la frecuencia angular.
- ωt+φ la fase.
- φ la fase inicial.
La partícula oscila alejándose y acercándose de un punto, situado en el centro de su trayectoria o punto de equilibrio, de tal manera que su posición en función del tiempo con respecto a ese punto es una sinusoide. En este movimiento, la fuerza que actúa sobre la partícula es proporcional a su desplazamiento respecto a dicho punto y dirigida hacia éste, esta fuerza en todo momento dirige a la partícula hacia su posición de equilibrio y recibe el nombre de fuerza restauradora. En el MAS la posición, la velocidad, la aceleración y la fuerza varían con la posición en función del tiempo.
En el movimiento armónico simple, la frecuencia y el periodo son independientes de la amplitud, y la aceleración es proporcional al desplazamiento, pero de sentido contrario:
Características de un M.A.S.
- Como los valores máximo y mínimo de la función seno o cos son +1 y -1, el movimiento se realiza en una región del eje X comprendida entre -A y +A.
- La función seno es periódica y se repite cada 2p, por tanto, el movimiento se repite cuando el argumento de la función seno o cos se incrementa en 2p, es decir, cuando transcurre un tiempo P tal que.
Parámetros fundamentales
El periodo T, es el tiempo que se requiere para efectuar una oscilación completa, esto es, para cada repetición sucesiva del movimiento de ida y vuelta, sus unidades en SI son segundos.La frecuencia f del movimiento, es el número de oscilaciones por unidad de tiempo, sus unidades en SI es Hz o 1/s, por consiguiente la frecuencia es el recíproco del periodo T. T = 1/f. Posición de equilibrio, es la posición para la cual no obra ninguna fuerza sobre la partícula, es generalmente donde se ubica el sistema de coordenadas para medir las distancias.Se llama elongación (lineal o angular) a la distancia (lineal o angular) de la partícula que oscila a su posición de equilibrio en cualquier instante, sus unidades en SI son m. La amplitud del movimiento A, es la máxima elongación.
Ecuación del movimiento
Elongación
Un resorte cuando lo separamos de su posición de equilibrio, estirándolo o comprimiéndolo, adquiere un movimiento vibratorio armónico simple, pues la fuerza recuperadora de ese resorte es la que genera una aceleración, la cual le confiere ese movimiento de vaivén. La posición que ocupa el bloque en cada momento con respecto al punto central la conocemos como ELONGACIÓN, x. Para definir el movimiento se calcula su ecuación, la relación entre las magnitudes que intervienen e influyen sobre él. Para encontrar una ecuación que relacione la posición (x) con el tiempo x(t),. Para ello se toman como punto de partida dos leyes muy conocidas en Física:
- Ley de Hooke: que determina que la fuerza recuperadora del resorte es proporcional a la posición y de signo contrario. La expresión de la ley es:
F = - Kx
- La 2ª ley de Newton: que relaciona la fuerza, la masa y la aceleración, cuya expresión es:
F = ma
Es obvio que la fuerza recuperadora del resorte es la que origina la aceleración del movimiento, lo que supone que ambas fuerzas, expresadas arriba, son iguales. Luego:
donde se expresa la aceleración como la segunda derivada de la posición con respecto al tiempo. La solución de esta ecuación para el valor de la posición en función del tiempo es:
siendo x(t) la elongación, A la amplitud o máxima elongación, ω la frecuencia angular y φ el desfase, que nos indica la discrepancia entre el origen de espacios (punto donde empezamos a medir el espacio) y el origen de tiempos.
El valor de la frecuencia angular está relacionado con la constante recuperadora por la ecuación que viene a continuación:
Velocidad
A partir de la ecuación de la posición o elongación) y, derivando con respecto al tiempo, obtenemos la ecuación de la velocidad en el MAS:
Modificando ligeramente esta e cuación encontramos una expresión de la velocidad en función de x, la elongación:
Aceleración
Derivando con respecto al tiempo la ecuación de velocidad, obtenemos la ecuación de la aceleración en el MAS:
de la que podemos obtener también una ecuación que la relaciona con la posición:
Amplitud y fase inicial
Conociendo la posición inicial x0 y la velocidad inicial v0 en el instante t=0.
se determinan la amplitud A y la fase inicial φ
Consideraciones energéticas en el MAS
Las fuerzas involucradas en un movimiento armónico simple son centrales y, por tanto, conservativas. En consecuencia, se puede definir un campo escalar llamado energía potencial (Ep) asociado a la fuerza. Para hallar la expresión de la energía potencial, basta con integrar la expresión de la fuerza (esto es extensible a todas las fuerzas conservativas) y cambiarla de signo, obteniéndose para el caso específico de un sistema de masa-resorte la siguiente expresión para la energía potencial :
Ep = ½ K x2
La energía potencial alcanza su máximo en los extremos de la trayectoria y tiene valor nulo (cero) en el punto x = 0, es decir el punto de equilibrio.
La energía cinética cambiará a lo largo de las oscilaciones pues lo hace la velocidad:
Ec = ½ mv2
La energía cinética es nula en -A o +A (v=0) y el valor máximo se alcanza en el punto de equilibrio (máxima velocidad Aω). Sustituyendo la ecuación de velocidad para el MAS podemos obtener la expresión para la energía cinética máxima como sigue.
Ec max = ½ ω2A2
Como sólo actúan fuerzas conservativas, la energía mecánica (suma de la energía cinética y potencial) permanece constante.
Ec + Ep = Em
Finalmente, al ser la energía mecánica constante, puede calcularse fácilmente considerando los casos en los que la velocidad de la partícula es nula y por lo tanto la energía potencial es máxima, es decir, en los puntos x = − A y x = A. Se obtiene entonces que,
Em = Ep max + 0 = ½ KA2
O también cuando la velocidad de la partícula es máxima y la energía potencial nula, en el punto de equilibrio x = 0
Em = 0 + Ec max = ½ ω2A2
Fuentes
- Microsoft ® Encarta ® 2008. © 1993--2007 Microsoft Corporation.
- http://es.wikipedia.org/wiki/Categoría:Movimiento_armónico_simple
- http://www.sc.ehu.es/sbweb/fisica/oscilaciones/mas/mas.htm
- http://usuarios.multimania.es/pefeco/mas/mas1.htm
- http://perso.wanadoo.es/cpalacio/mas2.htm