Rectas paralelas
| ||||
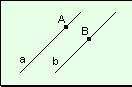
Rectas paralelas. Son dos rectas que no tienen ningún punto en común, o son coincidentes. Dos rectas, contenidas en un plano, son paralelas si o bien son una y la misma recta (son rectas coincidentes) o, por el contrario, no comparten ningún punto. De manera semejante, en el espacio, dos planos son paralelos si bien son uno y el mismo plano o bien no comparten ningún punto.
Sumario
Definición de Recta
Una Recta es una sucesión infinita de puntos, situados todos en una misma dirección, en tanto, esa sucesión se caracteriza por ser continua e indefinida, por tanto, una recta no tiene ni principio ni fin; junto al plano y al punto, la recta es uno de los entes geométricos fundamentales.
- Una recta es una sucesión infinita de puntos, situados en una misma dirección.
- Una recta tiene una sola dimensión: la longitud.
- Las rectas se nombran mediante dos de sus puntos o por una letra minúscula. **Dos puntos determinan una recta.
Definiciones de Rectas Paralelas
Axioma de unicidad
El axioma que distingue a la Geometría euclídea de otras geometrías es el siguiente: En un plano, por un Punto exterior a una Recta pasa una y sólo una paralela a dicha recta.
- Rectas paralelas son aquellas rectas que se encuentran en un mismo plano, presentan la misma pendiente y que no presentan ningún punto en común, esto significa que no se cruzan, ni tocan y ni siquiera se van a cruzar sus prolongaciones. Uno de los ejemplos más populares es el de las vías de un tren.
- Dos rectas son paralelas si sus vectores directores son paralelos, es decir, si éstos son linealmente dependientes.
- Dos rectas son paralelas si tienen sus vectores directores iguales.
- Dos rectas son paralelas si tienen sus pendientes iguales.
- Dos rectas son paralelas si los coeficientes de x e y respectivos son proporcionales.
- Dos rectas son paralelas si forman un ángulo de 0º.
Propiedades de las Rectas Paralelas
Las propiedades que ostentan las mismas son:
- Reflexiva (toda recta es paralela a si misma)
- Simétrica (si una recta es paralela a otra, aquella será paralela a la primera)
- Transitiva (si una recta es paralela a otra y esta a su vez es paralela a una tercera, la primera será paralela a la tercera recta),
- corolario de la propiedad transitiva (dos rectas paralelas a una tercera serán paralelas entre sí) y (todas las rectas paralelas presentan la misma dirección)
En tanto, los teoremas vinculados a las rectas paralelas nos dicen: que en un plano, dos rectas perpendiculares a una tercera serán paralelas entre sí; por un punto exterior a una recta, pasará siempre una paralela a esa recta; y si una recta corta a una de dos paralelas, cortará también a la otra, siempre hablando en un plano. El trazado de las líneas paralelas puede llevarse a cabo con regla y escuadra o con regla y compás.
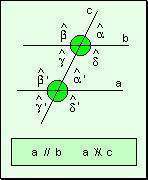
Ángulos determinados por dos rectas paralelas cortadas por una transversal
Dos rectas cualesquiera cortadas por una tercera determinan ocho ángulos.
Clasificación
De acuerdo a la ubicación de los mismos se clasifican en:
- Ángulos interiores: Están ubicados en la zona comprendida entre las rectas paralelas .
- Ángulos exteriores: Los ángulos que no son interiores se denominan ángulos exteriores.
- Ángulos correspondientes: Si dos ángulos están ubicados de un mismo lado de la transversal, uno es interior y el otro es exterior, se les llama ángulos correspondientes.
- Los ángulos correspondientes entre paralelas son iguales.
- Recíprocamente, si dos rectas cortadas por una tercera forman ángulos correspondientes iguales, las rectas son paralelas.
- Ángulos alternos:
- Ángulos alternos internos: Si dos ángulos están situados en distintos semiplanos con respecto a la transversal y ambos son internos, se les llama ángulos alternos internos.
- Los ángulos alternos internos entre paralelas son iguales. Recíprocamente, si dos rectas cortadas por una tercera forman ángulos alternos internos iguales, las rectas son paralelas.
- Ángulos alternos externos: Si dos ángulos están situados en distintos semiplanos con respecto a la transversal y ambos son externos, se les llama ángulos alternos externos.
- Los ángulos alternos internos entre paralelas son iguales. Recíprocamente, si dos rectas cortadas por una tercera forman ángulos alternos externos iguales, las rectas son paralelas.
- Ángulos conjugados
- Ángulos conjugados internos: Si dos ángulos están situados en un mismo semiplano con respecto a la transversal y ambos son internos, se les llama ángulos conjugados internos.
Los ángulos conjugados internos entre paralelas son suplementarios. Recíprocamente, si dos rectas cortadas por una tercera forman ángulos conjugados internos suplementarios, las rectas son paralelas.
- Ángulos conjugados externos: Si dos ángulos están situados en un mismo semiplano con respecto a la transversal y ambos son externos, se les llama ángulos conjugados externos.