Ángulo
Ángulo. En Geometría y Trigonometría, ángulo (por completo, ángulo plano) es la figura formada por dos rayos al compartir un campo común o punto final, llamado cima del ángulo. La magnitud del ángulo es la “cantidad de rotación” que separe los dos rayos, y puede ser medida considerando la longitud del Arco circular barrida hacia fuera cuando un rayo se rota sobre la cima para coincidir con el otro. El término “ángulo” se utiliza alternativamente para la configuración geométrica de sí mismo y para su magnitud angular (que sea simplemente una cantidad numérica).
La palabra ángulo viene de Latino palabra angulus, significando “una esquina”. La palabra angulus es un diminutivo, del cual la forma primitiva, angus, no existe en Latín. En el latín angere, significa “comprimir una curva” o “estrangular”, en Griego ἀγκύλος (ankylοs), significa “torcido, curvado,” y en Inglés la palabra significa “tobillo"; todos están conectados con Proto-Indo-Europeo raíz *ank-, significando “doblarse” o “arquearon”.
Sumario
Antecedentes
Euclides define un ángulo como la inclinación de un plano a otro, dos líneas que se satisfagan, y no pierde derecho con respecto a uno otro. Según Proclus un ángulo debe ser una calidad o una cantidad, o una relación. El primer concepto fue utilizado por Eudemus, que miró un ángulo como desviación de una línea recta; el segundo fue Carpo de Antioch, que lo miró como el intervalo o el espacio entre las líneas que se intersecaban; Euclides adoptó el tercer concepto, aunque sus definiciones de ángulos derechos, agudos, y obtusos son ciertamente cuantitativas.
El origen del término geometría es una descripción precisa del trabajo de los primeros geómetras, que se interesaban en problemas como la medida del tamaño de los campos o el trazado de ángulos rectos para las esquinas de los edificios. Este tipo de geometría empírica, que floreció en el Antiguo Egipto, Sumeria y Babilonia, fue refinado y sistematizado por los griegos.
Pitágoras
En el siglo VI a.C. el matemático Pitágoras colocó la piedra angular de la geometría científica al demostrar que las diversas leyes arbitrarias e inconexas de la geometría empírica se pueden deducir como conclusiones lógicas de un número limitado de axiomas, o postulados.
Estos postulados fueron considerados por Pitágoras y sus discípulos como verdades evidentes; sin embargo, en el pensamiento matemático moderno se consideran como un conjunto de supuestos útiles pero arbitrarios. Un ejemplo típico de los postulados desarrollados y aceptados por los matemáticos griegos es la siguiente afirmación: "una línea recta es la distancia más corta entre dos puntos".
Un conjunto de teoremas sobre las propiedades de puntos, líneas, ángulos y planos se puede deducir lógicamente a partir de estos axiomas. Entre estos teoremas se encuentran: "la suma de los ángulos de cualquier triángulo es igual a la suma de dos ángulos rectos", y "el cuadrado de la hipotenusa de un triángulo rectángulo es igual a la suma de los cuadrados de los otros dos lados" (conocido como teorema de Pitágoras).
Ángulos que miden
Para medir un ángulo θ, o arco circular centrado en la cima del ángulo se dibuja con un compás. La longitud del arco entonces es dividida por el radio del círculo r, y multiplicado posiblemente por una constante del escalamiento k (que depende de las unidades de medida que se eligen ).
El valor de θ se define independiente del tamaño del círculo: si la longitud del radio entonces se cambia la longitud del arco cambia en la misma proporción, tan el cociente s/r es inalterado. En muchas situaciones geométricas, los ángulos que diferencian por un múltiplo exacto de un círculo completo son con eficacia equivalente (no diferencia ningún cuántas veces una línea se rota a través de un círculo completo porque termina siempre para arriba en el mismo lugar).
Sin embargo, éste no es siempre el caso. Por ejemplo, al remontar una curva tal como a espiral el usar coordenadas polares, una vuelta completa adicional da lugar a un punto absolutamente diverso en la curva.
Unidades
Los ángulos se consideran sin dimensiones, puesto que se definen como el cociente de longitudes. Hay, sin embargo, varias unidades usadas para medir ángulos, dependiendo de la opción de la constante k en la fórmula arriba. De estas unidades, tratado más detalladamente abajo, grado y radián están en gran medida el más común.
Con la excepción notable del radián, la mayoría de las unidades de la medida angular se definen tales que un círculo completo (es decir. una revolución) es igual a n unidades, para un cierto número entero n. Por ejemplo, en el caso de grados, n = 360°. Un círculo completo de n las unidades son obtenidas fijando k = n/(2π) en la fórmula arriba. (Prueba. El fórmula arriba se puede reescribir como k = θr/s. Un círculo completo, para el cual θ = n las unidades, corresponden a un arco igual de la longitud del círculo de la circunferencia, que es 2πr, tan s = 2πr. Al sustituir θ por n y s por 2πr la fórmula, da lugar a k = nr/(2πr) = n/(2π).)
- grado, denotado por un círculo pequeño del exponente (°) es 1/360 de un círculo completo, así que un círculo completo es 360°. Una ventaja de este viejo sistema sexagesimal en la subunidad es que muchos ángulos comunes en geometría siempre son en su totalidad números medidos en grados, pero las subunidades sexagesimales siguientes del “grado-minuto-segundo” son utilizadas especialmente para coordenadas geográficas y eastronomía y balística.
- minuto del arco (o MOA, arcminute, o apenas minuto) es 1/60 de un grado. Es denotado por una sola prima (′). Por ejemplo, el ′ 3° 30 es igual 3 + 30/60 grado, o 3.5 grados. Un formato mezclado con las fracciones decimales también se utiliza a veces, e.g. ′ 3° 5.72 = 3 + 5.72/60 grados. A milla náutica fue definido históricamente como minuto del arco a lo largo de a gran círculo de la tierra.
- el segundo lugar del arco (o arcsecond, o apenas en segundo lugar) es 1/60 de un minuto del arco y 1/3600 de un grado. Es denotado por una prima doble (″). Por ejemplo, 3° 7 el ″ del ′ 30 es igual 3 + 7/60 + 30/3600 grado, o 3.125 grados.
- radián es el ángulo sostenido por un arco en un círculo que tenga la misma longitud que el radio del círculo (k = 1 en el fórmula dado anterior). Un círculo completo es 2π los radianes, y un radián es 180/π grados, o cerca de 57.2958 grados. Se abrevia el radián rad, aunque este símbolo se omite a menudo en los textos matemáticos, donde los radianes se asumen salvo especificación de lo contrario. El radián se utiliza en virtualmente todo el trabajo matemático más allá de la geometría práctica simple, debido a las características “naturales” de funciones trigonométricas cuando están expresadas en radianes. El radián es la unidad (derivada) de la medida angular en SI de medidas
- mili pulgada es aproximadamente igual a mili radián.
- círculo completo (o revolución, rotación, por completo vuelta o ciclo) es una revolución completa. Se abrevian la revolución y la rotación revolución y putrefacción, respectivamente, pero apenas r en RPM (revoluciones por minuto). 1 círculo = 360° llenos = 2π rad = gon 400 = 4 ángulos rectos.
- ángulo recto es 1/4 de un círculo completo. 1 ángulo recto = 90° = π/2 rad = gon 100.
- ángulo del triángulo equilátero es 1/6 de un círculo completo. Era la unidad usada por Babilónico, y es especialmente fácil de construir con la regla y los compases. El grado, minuto del arco y del arco está en segundo lugar sexagesimal subunidades de la unidad babilónica. 1 unidad = 60° babilónicos = π≈ de /3 rad 1.047197551 rad.
- grad, también llamado grado, gradian, o gon es 1/400 de un círculo completo, así que un círculo completo es 400 grads y a ángulo recto son 100 grads. Es una subunidad decimal del ángulo recto. A kilómetro fue definido históricamente como a centi- el gon del arco a lo largo de un gran círculo de la tierra, así que el kilómetro es el análogo decimal a la milla náutica sexagesimal. El gon se utiliza sobre todo en triangulación.
- punto, utilizado adentro navegación, es 1/32 de un círculo completo. Es una subunidad binaria del círculo completo. Nombramiento de los 32 puntos en a el compás se levantó se llama “encajonamiento del compás". 1 punto = 1/8 de un ángulo recto = de un 11.25° = gon 12.5.
- En Astronomía el ángulo de la hora es 1/24 de un círculo completo. Las subunidades sexagesimal fueron llamadas minuto de tiempo y en segundo lugar del tiempo (aun cuando son unidades del ángulo). 1 hora = 15° = π/12 rad = 1/6 gon del ≈ 16.667 del ángulo recto.
- grado binario, también conocido como radián binario (o alfilerillo), es 1/256 de un círculo completo. El grado binario se utiliza en computar para poder representar eficientemente un ángulo en un solo objeto.
- grado de una cuesta, o gradiente, no es una medida del ángulo (a menos que se da explícitamente grados). Al igual es la tangente del ángulo, o a veces el seno. Los gradientes se expresan a menudo como porcentaje. Para los valores pequeños generalmente encontrados (menos del 5%), el grado de una cuesta es aproximadamente la medida de un ángulo en radianes.
Ángulos positivos y negativos
Una convención adoptada universal en la escritura matemática es que son los ángulos dados una muestra ángulos positivos si está medido a la izquierda, y ángulos negativos si está medido a la derecha, de una línea dada. Si no se especifica ninguna línea, puede ser asumido para ser x-axis en Plano cartesiano. En muchas situaciones geométricas un ángulo negativo del −θ está con eficacia el equivalente a un ángulo positivo de “una rotación completa menos θ". Por ejemplo, una rotación a la derecha de 45° (es decir, un ángulo de −45°) es a menudo con eficacia equivalente a una rotación a la izquierda 360° del − 45° (es decir, un ángulo de 315°). En geometría tridimensional, “a la derecha” y “a la izquierda” no tenga ningún significado absoluto, así que la dirección de ángulos positivos y negativos se debe definir concerniente a una cierta referencia, que es típicamente a un vector al pasar por la cima del ángulo y perpendicular al plano. En navegación, cojinetes se miden del norte, aumentando a la derecha, así que un cojinete de 45 grados es de nordeste. Los cojinetes negativos no se utilizan en la navegación, así que el noroeste es 315 grados.
Aproximaciones
- 1° es aproximadamente la anchura de un pequeño dedo en la longitud del brazo
- 10° es aproximadamente la anchura de un puño cerrado en la longitud del brazo.
- 20° es aproximadamente la anchura de un handspan en la longitud del brazo.
Identificar ángulos
En expresiones matemáticas, es común al uso Letras griegas (α, β, γ, θ, φ,…) para servir como variables; para expresar el tamaño de un cierto ángulo.
En figuras geométricas, los ángulos se pueden también identificar por las etiquetas unidas a los tres puntos que los definen.
Por ejemplo, el ángulo en la cima A incluida por los rayos AB y CA (es decir. las líneas del punto A al punto B y señalan A al punto C) son ∠BAC denotado o BÂC. A veces, donde no hay riesgo de la confusión, el ángulo se puede referir simplemente por su cima . Potencialmente, un ángulo se denota, por ejemplo, el ∠BAC se puede referir a cualesquiera de cuatro ángulos: el ángulo a la derecha de B de C, el ángulo contrario al reloj de B de C, el ángulo a la derecha de C de B, o el ángulo contrario al reloj de C de B, donde la dirección en la cual se mide el ángulo determina su muestra.Una convención puede ser adoptada de modo que el ∠BAC refiera siempre al ángulo (positivo) contrario al reloj de B de C, y ∠CAB al ángulo (positivo) contrario al reloj de C del B.
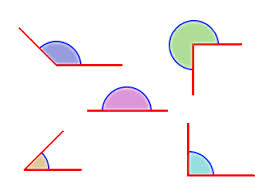
Clasificación de ángulos según su amplitud
Clasificación de los Ángulos segun su tipo y amplitud...
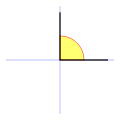
• Un ángulo de 90° (πlos radianes de /2, o un cuarto del círculo completo) se llama a ángulo recto. Dos líneas que forman un ángulo recto serían perpendicular o orthogonal.
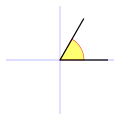
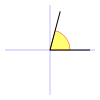
• Los ángulos más pequeños que un ángulo recto (menos que 90°) se llaman ángulos agudos (significado “agudo” “sostenido”).
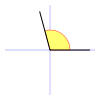
• Los ángulos más grandes que un ángulo recto y más pequeño de dos ángulos rectos (entre 90° y 180°) se llaman ángulos obtusos (el significado “obtuso” “blunt”).
• Los ángulos iguales a dos ángulos rectos (180°) se llaman ángulos rectos.
• Se llaman los ángulos más en gran parte de dos ángulos rectos pero menos que un círculo completo (entre 180° y 360°) ángulos reflejos.
• Los ángulos que tienen la misma medida son congruentes o iguales.
• Dos ángulos formados por dos líneas rectas que se intersecan, que formen una “X” en su representación, se llaman ángulos verticales o ángulos opuestos por el vértice. Estos ángulos son congruentes o iguales.
•Se llaman los ángulos que comparten una cima y un borde comunes pero no comparten ningún punto interior ángulos adyacentes.
• Se llaman dos ángulos que suman un ángulo recto (90°) ángulos complementarios.La diferencia entre un ángulo y un ángulo recto se llama complemento del ángulo.
• Se llaman dos ángulos que suman a un ángulo recto (180°) ángulos suplementarios. La diferencia entre un ángulo y un ángulo recto se llama suplemento del ángulo.
• Se llaman dos ángulos que suman a un círculo completo (360°)ángulos conyugales.
• Un ángulo que es parte de un polígono simple se llama ángulo interior de ese polígono simple. Observe que en un polígono simple que sea cóncavo, por lo menos un ángulo interior excede 180°.
En Geometría Euclideana, la suma de los ángulos interiores de un triángulo es de π radianes, o 180°; la suma de los ángulos interiores de un simple cuadrilátero es de 2π radianes, o 360°.
• El ángulo suplementario del ángulo interior se llama ángulo exterior. Mide la cantidad de la “vuelta” que tiene que hacer en esta cima para remontar hacia fuera el polígono. Si el ángulo interior correspondiente excede 180°, el ángulo exterior debe ser considerado negativo. Incluso en un polígono no-simple puede ser posible definir el ángulo exterior, pero uno tendrá que escoger orientación de plano (o superficie) para decidir la muestra de la medida exterior del ángulo.
Galería de ángulos
Aplicaciones de los ángulos en la Geografía y en la Astronomía
En Geografía, se especifica la localización de cualquier punto en la tierra usando el Sistema de Coordenadas Geográficas. Este sistema especifica latitud y longitud de cualquier localización, en términos de ángulos sostenidos en el centro de la Tierra, al usar ecuador y (generalmente) Meridiano de Greenwich como referencias.
En Astronomía, se especifica un punto dado en la esfera celestial usando ualesquiera de los varios Sistemas de Coordenadas Astronómicas, donde las referencias varían según el sistema particular. Los astrónomos pueden también medir separación angular de dos estrellas imaginando dos líneas a través del centro del Tierra, cada uno que interseca una de las estrellas. El ángulo entre esas líneas se puede medir, y es la separación angular entre las dos estrellas. Los astrónomos también miden tamaño evidente de objetos. Por ejemplo, la Luna Llena tiene una medida angular de aproximadamente 0.5°, cuando está visto de la Tierra. Uno podía decir, “los sostenidos de la luna un ángulo de la mitad del grado.”