Series Matemáticas
| ||||
Series Matemáticas . Una serie es la suma de los términos de una sucesión: ![]()
Se representa una serie con términos an como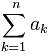 donde n es el índice final de la serie.
donde n es el índice final de la serie.
Las series convergen si  para algún
para algún ![]() , divergen si
, divergen si 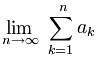 no existe o si tiende a infinito.
no existe o si tiende a infinito.
Sumario
- 1 Tipos de series
- 2 Criterios de convergencia
- 3 Convergencia absoluta y condicional
- 4 Fuente
- 5 Véase también
Tipos de series
Serie geométrica
Una serie geométrica es aquella cuyos términos forman una progresión geométrica. (Cada término es igual al anterior multiplicado por una constante). La fórmula de una serie geométrica siempre se puede escribir en la forma normal:
Serie armónica
La serie armónica es la serie:
 . La serie armónica es divergente.
. La serie armónica es divergente.
Serie alternada
Una serie alternada es aquella cuyos términos son alternativamente positivos y negativos. Ejemplo:
Serie de potencias
•Una serie de potencias alrededor de x=0 es una serie de la forma: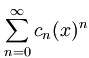
Una serie de potencias alrededor de x=a es una serie de la forma:
En el cual el centro es a, y los coeficientes Cn son constantes.
Serie telescópica
Una serie telescópica es la suma ![]() , donde
, donde ![]() . Se representa de la siguiente manera:
. Se representa de la siguiente manera:
Criterios de convergencia
Condición necesaria para la convergencia
Teorema
Es condición necesaria para que la serie 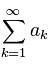 sea convergente, que
sea convergente, que ![]()
Nota: Este criterio es necesario pero no suficiente, es decir que, si el término n-ésimo tiende a 0, no se puede afirmar que la serie sea convergente.
Condición suficiente
Para que una serie 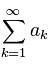 sea divergente, una condición suficiente es que
sea divergente, una condición suficiente es que ![]() .
.
Esta afirmación es muy útil, ya que nos ahorra trabajo en los criterios cuando el límite es distinto de cero.
Criterio de Alembert o Criterio del Cociente
Sea una serie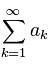 , tal que ak > 0 ( serie de términos positivos).
, tal que ak > 0 ( serie de términos positivos).
Si existe 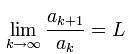 con
con ![]() , el Criterio de D'Alembert establece que:
, el Criterio de D'Alembert establece que:
• si L < 1, la serie converge.
• si L > 1, entonces la serie diverge.
• si L = 1, no es posible decir algo sobre el comportamiento de la serie. En este caso, es necesario probar otro criterio.
Criterio de la raíz o de Cauchy
Sea una serie 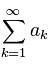 , tal que ak > 0 (serie de términos positivos). Y supongamos que existe
, tal que ak > 0 (serie de términos positivos). Y supongamos que existe![]() , siendo
, siendo ![]()
Entonces, si:
• L < 1, la serie es convergente.
• L > 1 entonces la serie es divergente.
• L=1, no es posible decir algo sobre el comportamiento de la serie. En este caso, es necesario probar otro criterio.
Criterio de Joseph Raaber
Sea una serie 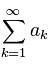 , tal que ak > 0 (serie de términos positivos). Y se supone que existe
, tal que ak > 0 (serie de términos positivos). Y se supone que existe![]() , siendo
, siendo ![]()
Por tanto, si L > 1, entonces la serie es convergente y si L < 1, la serie es divergente.
Criterio de la integral de Cauchy
Si la función f(x) es positiva, continua y decreciente en el intervalo [1, ∞) tal que f(n) = an para todo n, entonces la serie ![]() y la integral impropia
y la integral impropia ![]() convergen o divergen simultaneamente.
convergen o divergen simultaneamente.
Criterio de Leibniz
Una serie de la forma ![]() (con
(con ![]() ) se llama alternada. Tal serie converge si se cumplen las siguientes condiciones:
) se llama alternada. Tal serie converge si se cumplen las siguientes condiciones:
b) La serie tiene que ser absolutamente decreciente es decir que: ![]()
Si esto se cumple, la serie![]() es condicionalmente convergente de lo contrario la serie diverge.
es condicionalmente convergente de lo contrario la serie diverge.
Nota:Se debe descartar primero la convergencia absoluta de ![]() antes de aplicar este criterio, usando los criterios para series positivas.
antes de aplicar este criterio, usando los criterios para series positivas.
Criterios de convergencia comparativos
Son aplicables en caso de disponer de otra serie ![]() tal que se conozca su condición, tal como la divergencia para la serie geométrica con razón (en valor absoluto) mayor que 1, |z| > 1. Entonces:
tal que se conozca su condición, tal como la divergencia para la serie geométrica con razón (en valor absoluto) mayor que 1, |z| > 1. Entonces:
Criterio de comparación directa ( de la mayorante o de Carl Friedrich Gauss )
Criterio de comparación por paso al límite del cociente
Entonces:
• Si L = 0 y ![]() converge
converge ![]() converge
converge
• En otro caso, ambas series comparten la misma condición (ambas convergen, o bien ambas son divergentes).
Convergencia absoluta y condicional
Convergencia absoluta
Se dice que la serie ![]() es absolutamente convergente si la serie de sus módulos
es absolutamente convergente si la serie de sus módulos ![]() es convergente.
es convergente.
Convergencia condicional
Se dice que la serie ![]() es condicionalmente convergente si
es condicionalmente convergente si ![]() converge, pero la serie de sus módulos
converge, pero la serie de sus módulos ![]() , diverge.
, diverge.
Fuente
Serpa,Alfredo. Series(2004). Editorial Félix Varela, La Habana.






