Vectores polares y vectores axiales
| ||||||
Vectores polares y vectores axiales. Al comparar entre sí los vectores representativos de la velocidad lineal de un punto material y el de la velocidad angular de rotación, advertimos que entre ellos existe una gran diferencia.
Sumario
Generalidades
La dirección del primer vector, representativo de la velocidad lineal del punto material está condicionada exclusivamente por el aspecto físico del fenómeno; es decir, la dirección del movimiento; la dirección del segundo vector (vector de la velocidad angular) depende, en cierto grado, de que la rotación se considere como positiva; esto es, que sea igual a la del movimiento de las manecillas del reloj o contraria a esa; en otras palabras, depende de la elección del sistema de coordenadas. Por tanto la dirección del segundo vector tiene un carácter convencional.
Los vectores pertenecientes al primer tipo se llaman polares y los del segundo tipo, axiales ó pseudovectores.
Vectores polares
Vectores polares son los vectores de la velocidad lineal y la aceleración lineal de un punto un material ect.
De la definición de producto vectorial se desprende que este representa en sí un vector axial. Pero esto es válido solamente cuando ambos vectores son vectores polares; si uno de los vectores es axial, entonces su producto vectorial es un vector polar. Así, por ejemplo, la velocidad lineal (vector polar) es el producto vectorial del radiovector del punto (vector polar) por la velocidad angular (vector axial).
Diferenciación gráfica de vectores
Formalmente, los vectores polares y axiales pueden distinguirse de la siguiente manera:
Si al pasar de un sistema directo a uno inverso, ó al revés, un vector permanece invariable; entonces este es un vector polar; si su sentido cambia al opuesto, el vector es axial.
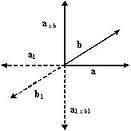
Como ejemplo examinemos el producto vectorial de dos vectores axiales. Al cambiar el sistema de coordenadas, los dos vectores cambian de sentido, tomando el sentido de la rotación del primer vector hacia el segundo, permanece como la primitiva, pero su producto vectorial, en virtud de su definición cambia su sentido por el opuesto.
Por consiguiente, el producto vectorial de dos vectores axiales es un vector axial como muestra la figura.
Al igual que con los vectores, los escalares también se dividen en dos tipos: escalares de primer tipo ó simplemente escalares; y esclares de segundo tipo ó pseudoescalares.
Estos últimos se obtienen por las operaciones entre vectores axiales y cambian de signo al pasar de un sistema a otro.
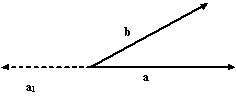
El producto escalar de un vector polar b por un vector axial a es un pseudoescalar como se muestra en la siguiente figura 2.
Véase también
Fuente
- Goldfan, I, A. Elementos de Cálculo Vectorial. Editado por Ciencia y Técnica, 1986. Traducción de profesores de la Escuela de Física de la Universidad de la Habana: ISBN 0-08-021680-3