Función Gamma

Función Gamma Concepto: Fórmula matemática utilizada en la generalización de la función factorial y el desarrollo de la transformada de Laplace. Tiene importantes aplicaciones en la teoría de las probabilidades y estadísticas.

Función Gamma Es una integral impropia, que no tiene solución analítica directa, con propiedades especiales que permiten su utilización en la generalización de la función factorial y el desarrollo de la transformada de Laplace. También se utiliza en estadísticas para el cálculo de funciones de distribución de probabilidad.

Definición

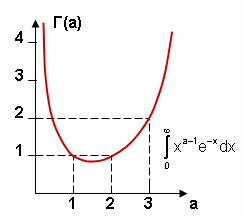
La función gamma de un número a > 0, se denota como Γ(a), es el resultado de la integral impropia:

La representación integral original de la función Ganma fue dada por Euler, razón por la cual a veces suele decirse que es una integral euleriana de segunda especie. También Adrien-Marie Legendre contribuyó al desarrollo de la función en el campo de los números complejos.

Propiedades

El desarrollo de la integral, para a número entero, conduce mediante la integración por partes a la importante conclusión:
Γ(a+1)=aΓ(a)
Esto permite plantear la equivalencia entre la función gamma y el factorial de un número entero como:
Γ(n)=(n-1)!
Con la ventaja de que gamma es una función continua y por tanto permite argumentos reales.

Fórmulas aproximadas

Dado que la función Gamma se incrementa muy rápidamente cuando crece el argumento, a veces es conveniente utilizar fórmulas aproximadas para Γ(a) cuando a es grande. Una de ellas es la importante fórmula de Stirling:

Además se destaca la fórmula multiplicativa que se basa en una interesante propiedad del producto de dos Γ consecutivas y cuya demostración está relacionada con la Fórmula de Euler:

Esta última conduce al valor notable:

Aplicaciones

La función gamma es de primordial importancia para las matemáticas y otras ciencias. El desarrollo de la teoría de las probabilidades y la estadística descansa sobre la utilización de esta función para calcular funciones de distribución como la distribución Chi cuadrado, t de Student y F de Fisher tal y como se muestran a continuación:



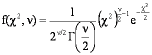
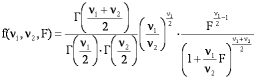
Adicionalmente, la función Ganma constituye la base fundamental de la Transformada de Laplace con aplicaciones importantes en la solución del ecuaciones integrales.

Fuentes

• Céspedes, Niguel y Díaz, José: Transformada de Laplace, Editorial Pueblo y Educación, La Habana, 1980.
• Wikipedia: Función Gamma
• Enciclopedia libre universal: Función Ganma
• Gaussianos.com: La función gamma, una generalización del factorial
• Enciclopedia Libre Universal: Función Gamma