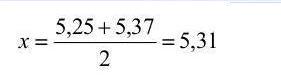Diferencia entre revisiones de «Error absoluto»
(Página creada con «{{Definición |nombre= El mínimo error absoluto máximo |imagen= |concepto= }} <div align="justify"> '''El mínimo error absoluto máximo'''. Sea x <sup>-</sup>una aproxim...») |
m (Texto reemplazado: «<div align="justify">» por «») |
||
| (No se muestran 5 ediciones intermedias de 2 usuarios) | |||
| Línea 4: | Línea 4: | ||
|concepto= | |concepto= | ||
}} | }} | ||
| − | + | ||
'''El mínimo error absoluto máximo'''. Sea x <sup>-</sup>una aproximación por defecto de x<sup>* </sup> y x <sup>+</sup> una aproximación por exceso del mismo número x<sup>* </sup>. Si x es cualquier número del intervalo [x <sup>-</sup>, x<sup>+</sup>], este número x será una aproximación de x<sup>* </sup> cuyo error absoluto máximo puede ser determinado fácilmente. | '''El mínimo error absoluto máximo'''. Sea x <sup>-</sup>una aproximación por defecto de x<sup>* </sup> y x <sup>+</sup> una aproximación por exceso del mismo número x<sup>* </sup>. Si x es cualquier número del intervalo [x <sup>-</sup>, x<sup>+</sup>], este número x será una aproximación de x<sup>* </sup> cuyo error absoluto máximo puede ser determinado fácilmente. | ||
| Línea 10: | Línea 10: | ||
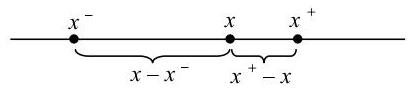
Para ello, considérese la figura 1. En ella se muestran las tres aproximaciones x <sup>-</sup>, x y x <sup>+</sup>. Como el verdadero valor x<sup>* </sup> pertenece al intervalo [x <sup>-</sup>, x <sup>+</sup>], entonces el error absoluto E(x) no puede exceder a la mayor de las dos distancias (x <sup>+</sup> - x) y (x -.x <sup>-</sup>) que determina x en el intervalo. | Para ello, considérese la figura 1. En ella se muestran las tres aproximaciones x <sup>-</sup>, x y x <sup>+</sup>. Como el verdadero valor x<sup>* </sup> pertenece al intervalo [x <sup>-</sup>, x <sup>+</sup>], entonces el error absoluto E(x) no puede exceder a la mayor de las dos distancias (x <sup>+</sup> - x) y (x -.x <sup>-</sup>) que determina x en el intervalo. | ||
| − | [[Imagen:figura1merror.JPG| | + | [[Imagen:figura1merror.JPG|center|figura 1]] |
| + | <center>figura 1</center> | ||
Es decir: E<sub>m </sub> (x) = max {x -.x <sup>-</sup>, x<sup>+</sup> -x} | Es decir: E<sub>m </sub> (x) = max {x -.x <sup>-</sup>, x<sup>+</sup> -x} | ||
De la figura resulta obvio que el error absoluto máximo tomará su mínimo valor si se escoge x justo en el centro del intervalo [x <sup>-</sup>, x<sup>+</sup>], en ese caso E<sub>m </sub> (x) será exactamente la semiamplitud del intervalo, esto es: | De la figura resulta obvio que el error absoluto máximo tomará su mínimo valor si se escoge x justo en el centro del intervalo [x <sup>-</sup>, x<sup>+</sup>], en ese caso E<sub>m </sub> (x) será exactamente la semiamplitud del intervalo, esto es: | ||
| − | S1 se toma | + | S1 se toma <br> |
[[Imagen:figura2merror.JPG]] | [[Imagen:figura2merror.JPG]] | ||
| + | |||
entonces se minimiza el error absoluto máximo, el cual será | entonces se minimiza el error absoluto máximo, el cual será | ||
| Línea 30: | Línea 32: | ||
E<sub>m </sub> (x) = max {5,3 -5,25; 5,37-5,3}= max {0,05; 0,07} =0,07 | E<sub>m </sub> (x) = max {5,3 -5,25; 5,37-5,3}= max {0,05; 0,07} =0,07 | ||
| − | El error absoluto máximo se minimiza tomando x en el centro del intervalo [5,25; 5,37], es decir: | + | El error absoluto máximo se minimiza tomando x en el centro del intervalo [5,25; 5,37], es decir:<br> |
| − | [[Imagen:figura4merror.JPG]] | + | [[Imagen:figura4merror.JPG]]<br> |
| − | Para ese valor de x, el error absoluto máximo será: | + | Para ese valor de x, el error absoluto máximo será:<br> |
[[Imagen:figura5merror.JPG]] | [[Imagen:figura5merror.JPG]] | ||
| − | |||
Obsérvese que esto no significa que 5,31 esté más próximo a x<sup>* </sup> que 5,3. Tan solo puede afirmarse que si se toma x = 5,3 como aproximación, el error absoluto podría llegar hasta 0,07 pero tomando x = 5,31 el error absoluto no puede pasar de 0,06. | Obsérvese que esto no significa que 5,31 esté más próximo a x<sup>* </sup> que 5,3. Tan solo puede afirmarse que si se toma x = 5,3 como aproximación, el error absoluto podría llegar hasta 0,07 pero tomando x = 5,31 el error absoluto no puede pasar de 0,06. | ||
última versión al 01:51 9 ago 2019
| ||
El mínimo error absoluto máximo. Sea x -una aproximación por defecto de x* y x + una aproximación por exceso del mismo número x* . Si x es cualquier número del intervalo [x -, x+], este número x será una aproximación de x* cuyo error absoluto máximo puede ser determinado fácilmente.
Determinar el error absoluto
Para ello, considérese la figura 1. En ella se muestran las tres aproximaciones x -, x y x +. Como el verdadero valor x* pertenece al intervalo [x -, x +], entonces el error absoluto E(x) no puede exceder a la mayor de las dos distancias (x + - x) y (x -.x -) que determina x en el intervalo.
Es decir: Em (x) = max {x -.x -, x+ -x}
De la figura resulta obvio que el error absoluto máximo tomará su mínimo valor si se escoge x justo en el centro del intervalo [x -, x+], en ese caso Em (x) será exactamente la semiamplitud del intervalo, esto es:
S1 se toma
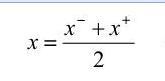
entonces se minimiza el error absoluto máximo, el cual será
Ejemplo
Se sabe que la raíz de una ecuación se encuentra en el intervalo [5,25; 5,37]. Si se torna como aproximación x = 5.3 ¿Cuál es el error absoluto máximo de esta aproximación? ¿Para qué valor de x se obtendría el menor error absoluto máximo`?
Solución:
De acuerdo con lo explicado anterionnente, para x = 5,3 se tiene:
Em (x) = max {5,3 -5,25; 5,37-5,3}= max {0,05; 0,07} =0,07
El error absoluto máximo se minimiza tomando x en el centro del intervalo [5,25; 5,37], es decir:
Para ese valor de x, el error absoluto máximo será:
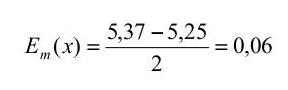
Obsérvese que esto no significa que 5,31 esté más próximo a x* que 5,3. Tan solo puede afirmarse que si se toma x = 5,3 como aproximación, el error absoluto podría llegar hasta 0,07 pero tomando x = 5,31 el error absoluto no puede pasar de 0,06.
Fuentes
MATEMÁTICA NUMERICA II EDICIÓN, Manuel Álvarez, Alfredo Guerra, Rogelio Lau