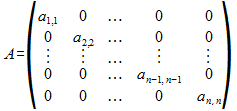Diferencia entre revisiones de «Matriz diagonal»

(→‎Véase también)
m (→‎Importancia: referencias)
 
(No se muestran 7 ediciones intermedias de 3 usuarios)
Línea 1: Línea 1:
 
{{Definición|Nombre=Matriz diagonal|imagen=MatrizDiagonalOrdenN.png|concepto=[[Matriz cuadrada]] cuyos elementos son [[cero]] a excepción de los de la diagonal principal.}}
 
{{Definición|Nombre=Matriz diagonal|imagen=MatrizDiagonalOrdenN.png|concepto=[[Matriz cuadrada]] cuyos elementos son [[cero]] a excepción de los de la diagonal principal.}}
  
−
<div align="justify">
 
−
'''Matriz diagonal'''. Dícese de la [[matriz cuadrada]] de orden N cuyos elementos excepto al menos uno de la diagonal principal son [[cero]].
 
  
−
Un caso particular de la [[matriz]] diagonal de orden N es la [[matriz identidad]].
+
'''Matriz diagonal'''. Denominación de la [[matriz cuadrada]] de orden ''n'' cuyos elementos, excepto al menos uno de la diagonal principal, son [[cero]].
 +
 
 +
Un caso especial e importante de la [[matriz]] diagonal de orden n es la [[matriz identidad]].
  
 
Es de gran utilidad en las [[aplicación lineal|aplicaciones lineales]] pues reducen notablemente el cálculo a una simple [[multiplicación]] directa.  
 
Es de gran utilidad en las [[aplicación lineal|aplicaciones lineales]] pues reducen notablemente el cálculo a una simple [[multiplicación]] directa.  
  
 
==Definición==
 
==Definición==
−
Sea ''A'' una matriz cuadrada de orden N, se dice que es una '''matriz diagonal''' si todos sus elementos satisfacen que:
+
Sea ''A'' una matriz cuadrada de orden n, se dice que es una '''matriz diagonal''' si todos sus elementos satisfacen que:
  
−
* Para ''i=1..N'' e ''j=1..N'' tal que ''a<sub>i,j</sub>=0''.
+
* Para 1≤ i, j≤n,  i ≠ j se tiene ''a<sub>i,j</sub>=0''.  
−
* Existe ''i=1..N'' tal que ''a<sub>i,i</sub>≠0''
+
* Existe ''i=1..n'' tal que ''a<sub>i,i</sub>≠0''
  
 
Es decir a excepción de al menos uno en la diagonal principal todos sus elementos son nulos.
 
Es decir a excepción de al menos uno en la diagonal principal todos sus elementos son nulos.
  
−
Esto convierte en particularidad el caso de que todos los elementos de la diagonal principal sean no nulos y en especial, el caso cuando todos los elementos de la diagonal principal son 1 la matriz diagonal es también la matriz identidad de orden N ''I<sub>N</sub>''.
+
Esto convierte en particularidad el caso de que todos los elementos de la diagonal principal sean no nulos y en especial, el caso cuando todos los elementos de la diagonal principal son 1 la matriz diagonal es nombrada la ''matriz identidad de orden n'', denotada por ''I<sub>n</sub>'';  llamada también ''matriz uno'' <ref> Serge Lang, Algebra lineal </ref>
  
 
==Propiedades==
 
==Propiedades==
Línea 25: Línea 25:
 
** Para todo ''a<sub>i,i</sub>=1''
 
** Para todo ''a<sub>i,i</sub>=1''
 
* ''|A|=a<sub>1,1</sub>a<sub>2,2</sub>...a<sub>n,n</sub>''
 
* ''|A|=a<sub>1,1</sub>a<sub>2,2</sub>...a<sub>n,n</sub>''
−
* Una matriz cuadrada de orden ''N'' es similar a una matriz diagonal si y sólo si tiene ''N'' [[vector propio|vectores propios]] linealmente independientes. Dicha matriz se dice que es diagonalizable.
+
* Una matriz cuadrada de orden ''N'' es similar a una matriz diagonal si y sólo si tiene ''N'' [[vector propio|vectores propios]] [[vector linealmente independiente|linealmente independientes]]. Dicha matriz se dice que es diagonalizable.
 
* Los elementos ''a<sub>i,i</sub>'' con ''i=1..N'' son [[valor propio|valores propios]] de ''A''.
 
* Los elementos ''a<sub>i,i</sub>'' con ''i=1..N'' son [[valor propio|valores propios]] de ''A''.
 
* Si existe el producto matricial ''C=AB'' con ''B'' de ''NxM'' los elementos de ''C'' serán de la forma ''c<sub>i,j</sub>=a<sub>i,i</sub>b<sub>i,j</sub>'' para ''i=1..N'' e ''j=1..M''.
 
* Si existe el producto matricial ''C=AB'' con ''B'' de ''NxM'' los elementos de ''C'' serán de la forma ''c<sub>i,j</sub>=a<sub>i,i</sub>b<sub>i,j</sub>'' para ''i=1..N'' e ''j=1..M''.
Línea 31: Línea 31:
  
 
==Importancia==
 
==Importancia==
−
La simplificación operatoria de las matrices hace que sean muy deseables en el caso de la representación o modelación de transformaciones lineales en el álgebra homónima. El llevar una matriz cuadrada a su similar diagonal es una garantía de simplicidad que en el caso del cálculo computacional.
+
La simplificación operatoria de las matrices hace que sean muy deseables en el caso de la representación o modelación de [[transformaciones lineales]] en el álgebra lineal y en ecuaciones diferenciales. El llevar una matriz cuadrada a su similar diagonal es un recurso de simplificación de todo tipo de cálculo matricial.
 +
 
 +
==Referencias==
 +
{{listaref}}
  
 
==Véase también==
 
==Véase también==

última versión al 12:43 5 sep 2019

Matriz diagonal
Información sobre la plantilla
MatrizDiagonalOrdenN.png
Concepto:Matriz cuadrada cuyos elementos son cero a excepción de los de la diagonal principal.


Matriz diagonal. Denominación de la matriz cuadrada de orden n cuyos elementos, excepto al menos uno de la diagonal principal, son cero.

Un caso especial e importante de la matriz diagonal de orden n es la matriz identidad.

Es de gran utilidad en las aplicaciones lineales pues reducen notablemente el cálculo a una simple multiplicación directa.

Definición

Sea A una matriz cuadrada de orden n, se dice que es una matriz diagonal si todos sus elementos satisfacen que:

  • Para 1≤ i, j≤n, i ≠ j se tiene ai,j=0.
  • Existe i=1..n tal que ai,i≠0

Es decir a excepción de al menos uno en la diagonal principal todos sus elementos son nulos.

Esto convierte en particularidad el caso de que todos los elementos de la diagonal principal sean no nulos y en especial, el caso cuando todos los elementos de la diagonal principal son 1 la matriz diagonal es nombrada la matriz identidad de orden n, denotada por In; llamada también matriz uno [1]

Propiedades

Sea una matriz diagonal A de orden N se cumple entonces:

  • A=IN si:
    • Para todos i=1..N e j=1..N e i≠j, ai,j=0.
    • Para todo ai,i=1
  • |A|=a1,1a2,2...an,n
  • Una matriz cuadrada de orden N es similar a una matriz diagonal si y sólo si tiene N vectores propios linealmente independientes. Dicha matriz se dice que es diagonalizable.
  • Los elementos ai,i con i=1..N son valores propios de A.
  • Si existe el producto matricial C=AB con B de NxM los elementos de C serán de la forma ci,j=ai,ibi,j para i=1..N e j=1..M.
  • Si existe el producto matricial C=BA con B de MxN los elementos de C serán de la forma ci,j=bi,jaj,j para i=1..M e j=1..N.

Importancia

La simplificación operatoria de las matrices hace que sean muy deseables en el caso de la representación o modelación de transformaciones lineales en el álgebra lineal y en ecuaciones diferenciales. El llevar una matriz cuadrada a su similar diagonal es un recurso de simplificación de todo tipo de cálculo matricial.

Referencias

  1. ↑ Serge Lang, Algebra lineal

Véase también

Fuentes

Obtenido de «https://www.ecured.cu/index.php?title=Matriz_diagonal&oldid=3546306»