Diferencia entre revisiones de «Distancia de un punto a una recta»
(Página creada con '{{Definición |nombre= Distancia de un punto a una recta |imagen= Punto.jpg |tamaño= |concepto= La distancia de un punto P(x1; y1) a la recta r de ecuación Ax + B...') |
m (Texto reemplazado: «<div align="justify">» por «») |
||
| (No se muestran 7 ediciones intermedias de 2 usuarios) | |||
| Línea 3: | Línea 3: | ||
|imagen= Punto.jpg | |imagen= Punto.jpg | ||
|tamaño= | |tamaño= | ||
| − | |concepto= La [[distancia]] de un punto | + | |concepto= La [[distancia]] de un punto P1(x1; y1) a la [[recta]] r de [[ecuación]] Ax + By + C = 0, se denota por d (P1; r) y es calculada mediante una fórmula. }} |
| − | |||
| − | |||
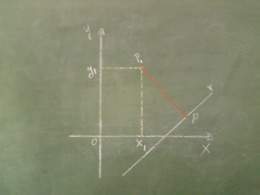
| + | '''Distancia de un punto a una recta'''. Al calcular la distancia de un punto P1 a una recta r, se determina la [[longitud]] del [[segmento]] perpendicular que une al punto P1 con la recta r. | ||
== Antecedentes históricos == | == Antecedentes históricos == | ||
| − | En el año 300 d.n.e. [[Pappus de Alejandría]] escribe su obra Colección y en ella plantea un problema que propone buscar el lugar geométrico formado por las intersecciones de rectas que satisfacen determinadas condiciones, pero no es hasta que el matemático [[René Descartes]] ([[1596]] - [[1650]]), intenta resolver el mismo problema y las ideas lo conducen a enlazar el [[Álgebra]] con la [[Geometría]]. Así surge la [[Geometría Analítica]]. Desde [[1628]] emplea Descartes sus procedimientos para resolver problemas de este tipo. | + | En el año [[300]] d.n.e. [[Pappus de Alejandría]] escribe su obra Colección y en ella plantea un problema que propone buscar el lugar geométrico formado por las intersecciones de rectas que satisfacen determinadas condiciones, pero no es hasta que el matemático [[René Descartes]] ([[1596]] - [[1650]]), intenta resolver el mismo problema y las ideas lo conducen a enlazar el [[Álgebra]] con la [[Geometría]]. Así surge la [[Geometría Analítica]]. Desde [[1628]] emplea Descartes sus procedimientos para resolver problemas de este tipo. |
Otro matemático que incursionó en esta rama de la [[Matemática]] y se consideró un digno rival de Descartes fue el francés [[Pedro Fermat]] ([[1601]] - [[1665]]). | Otro matemático que incursionó en esta rama de la [[Matemática]] y se consideró un digno rival de Descartes fue el francés [[Pedro Fermat]] ([[1601]] - [[1665]]). | ||
[[Image:Formula.jpg|thumb|rigth|185x141px|Fórmula para calcular la distancia de un punto P a una recta r]] | [[Image:Formula.jpg|thumb|rigth|185x141px|Fórmula para calcular la distancia de un punto P a una recta r]] | ||
| Línea 15: | Línea 14: | ||
== Características == | == Características == | ||
| − | * La fórmula se utiliza para calcular la distancia de un punto P a una recta r, si se conocen las coordenadas del punto y la ecuación de la recta. | + | * La fórmula se utiliza para calcular la distancia de un punto '''P''' a una recta '''r''', si se conocen las coordenadas del punto y la ecuación de la recta. |
| − | * Se emplea para resolver múltiples problemas de la Geometría Analítica cuando se combina con otras fórmulas dentro de ella. | + | * Se emplea para resolver múltiples problemas de la [[Geometría Analítica]] cuando se combina con otras fórmulas dentro de ella. |
| − | ==Ejemplos== | + | ===Ejemplos=== |
| − | *Cuando se quiere calcular la longitud de la altura relativa a un lado en un triángulo, si se conocen las coordenadas de los tres vértices | + | *Cuando se quiere calcular la longitud de la altura relativa a un lado en un [[triángulo]], si se conocen las coordenadas de los tres vértices |
*Cuando se quiere calcular la distancia entre dos rectas, si se conocen sus ecuaciones. | *Cuando se quiere calcular la distancia entre dos rectas, si se conocen sus ecuaciones. | ||
| Línea 27: | Línea 26: | ||
== Fuente == | == Fuente == | ||
| − | + | #Campistrous, L. et al ([[1990]]): Matemática 11. Grado. [[La Habana]]. [[Editorial Pueblo y Educación]]. | |
[[Category: Geometría analítica]] | [[Category: Geometría analítica]] | ||
[[Category: Matemáticas]] | [[Category: Matemáticas]] | ||
última versión al 17:01 5 ago 2019
| ||||||
Distancia de un punto a una recta. Al calcular la distancia de un punto P1 a una recta r, se determina la longitud del segmento perpendicular que une al punto P1 con la recta r.
Antecedentes históricos
En el año 300 d.n.e. Pappus de Alejandría escribe su obra Colección y en ella plantea un problema que propone buscar el lugar geométrico formado por las intersecciones de rectas que satisfacen determinadas condiciones, pero no es hasta que el matemático René Descartes (1596 - 1650), intenta resolver el mismo problema y las ideas lo conducen a enlazar el Álgebra con la Geometría. Así surge la Geometría Analítica. Desde 1628 emplea Descartes sus procedimientos para resolver problemas de este tipo. Otro matemático que incursionó en esta rama de la Matemática y se consideró un digno rival de Descartes fue el francés Pedro Fermat (1601 - 1665).
Características
- La fórmula se utiliza para calcular la distancia de un punto P a una recta r, si se conocen las coordenadas del punto y la ecuación de la recta.
- Se emplea para resolver múltiples problemas de la Geometría Analítica cuando se combina con otras fórmulas dentro de ella.
Ejemplos
- Cuando se quiere calcular la longitud de la altura relativa a un lado en un triángulo, si se conocen las coordenadas de los tres vértices
- Cuando se quiere calcular la distancia entre dos rectas, si se conocen sus ecuaciones.
Fuente
- Campistrous, L. et al (1990): Matemática 11. Grado. La Habana. Editorial Pueblo y Educación.