Diferencia entre revisiones de «Radián»
| (No se muestran 3 ediciones intermedias del mismo usuario) | |||
| Línea 1: | Línea 1: | ||
{{Definición | {{Definición | ||
|nombre=Radián | |nombre=Radián | ||
| − | |imagen= | + | |imagen=Rad1.png |
}} | }} | ||
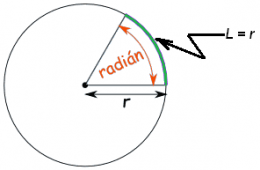
'''Radián'''. Es la unidad de [[ángulo]] plano en el [[Sistema Internacional de Unidades]]. Representa el [[ángulo]] central en una [[circunferencia]] que subtiende un arco cuya longitud es igual a la del radio. Su símbolo es '''''rad'''''. | '''Radián'''. Es la unidad de [[ángulo]] plano en el [[Sistema Internacional de Unidades]]. Representa el [[ángulo]] central en una [[circunferencia]] que subtiende un arco cuya longitud es igual a la del radio. Su símbolo es '''''rad'''''. | ||
== ''' Definición''' == | == ''' Definición''' == | ||
| − | |||
El [[ángulo]] formado entre dos semi rectas( cuya longitud es igual al radio de una circunferencia), es igul a la laongitud del arco que la delimitan dividido por el radio. Es decir: <big>'''''θ'''''</big> '''= l / r''', donde ('''''θ''''') es el ángulo, ('''''l''''') es la longitud del árco, ('''''r''''') es el radio del arco. | El [[ángulo]] formado entre dos semi rectas( cuya longitud es igual al radio de una circunferencia), es igul a la laongitud del arco que la delimitan dividido por el radio. Es decir: <big>'''''θ'''''</big> '''= l / r''', donde ('''''θ''''') es el ángulo, ('''''l''''') es la longitud del árco, ('''''r''''') es el radio del arco. | ||
| Línea 12: | Línea 11: | ||
Para determinar la medida en radianes de una circunferencia completa puede hacerce traves de la fórmula siguiente: | Para determinar la medida en radianes de una circunferencia completa puede hacerce traves de la fórmula siguiente: | ||
[[Archivo:Cir1.png|300px]]. Donde ('''''L''''') y ('''''r''''') son la longitud y radio de la circunferencia respectivamente | [[Archivo:Cir1.png|300px]]. Donde ('''''L''''') y ('''''r''''') son la longitud y radio de la circunferencia respectivamente | ||
| − | |||
== '''Utilidad''' == | == '''Utilidad''' == | ||
| Línea 22: | Línea 20: | ||
La equivalencia entre grados sexagesimales y radianes es: | La equivalencia entre grados sexagesimales y radianes es: | ||
'''<big>''π rad = 180°''</big>''' | '''<big>''π rad = 180°''</big>''' | ||
| − | |||
| − | |||
| − | |||
==Conversiones entre grados y radianes== | ==Conversiones entre grados y radianes== | ||
| Línea 34: | Línea 29: | ||
De radianes a grado | De radianes a grado | ||
| − | [[Archivo: | + | [[Archivo:RadGr1.png|90px ]] |
Donde <big>'''α'''</big> es el ángulo medido en radianes o grado; '''''π''''' =3.14.16. | Donde <big>'''α'''</big> es el ángulo medido en radianes o grado; '''''π''''' =3.14.16. | ||
última versión al 11:51 2 abr 2013
| ||||
Radián. Es la unidad de ángulo plano en el Sistema Internacional de Unidades. Representa el ángulo central en una circunferencia que subtiende un arco cuya longitud es igual a la del radio. Su símbolo es rad.
Sumario
Definición
El ángulo formado entre dos semi rectas( cuya longitud es igual al radio de una circunferencia), es igul a la laongitud del arco que la delimitan dividido por el radio. Es decir: θ = l / r, donde (θ) es el ángulo, (l) es la longitud del árco, (r) es el radio del arco.
Para determinar la medida en radianes de una circunferencia completa puede hacerce traves de la fórmula siguiente: 300px. Donde (L) y (r) son la longitud y radio de la circunferencia respectivamente
Utilidad
El radián es una unidad sumamente útil para medir ángulos, puesto que simplifica los cálculos, ya que los más comunes se expresan mediante sencillos múltiplos o divisores de π.
Equivalencias
La equivalencia entre grados sexagesimales y radianes es: π rad = 180°
Conversiones entre grados y radianes
Un ángulo puede ser expresado en radianes o grado, por lo que para convertirlo de de grado a radianes y viceversa podemos utilizar las siguientes fórmulas:
Donde α es el ángulo medido en radianes o grado; π =3.14.16.
Fuentes
- LT. Matemática 10mo grado. Colectivo de autores
- Enciclopedia encarta
- Matemática 4to curso. Geometría. De Antonio Páz