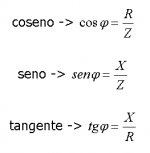Diferencia entre revisiones de «Impedancia»
m (Texto reemplazado: «<div align="justify">» por «») |
|||
| (No se muestran 38 ediciones intermedias de 3 usuarios) | |||
| Línea 3: | Línea 3: | ||
|imagen=ZZZ.jpeg | |imagen=ZZZ.jpeg | ||
|tamaño= | |tamaño= | ||
| − | |concepto=Magnitud física que aparece en los circuitos de corriente alterna y se caracterizada | + | |concepto=Magnitud física que aparece en los circuitos de [[corriente alterna]] y se caracterizada por ofrecer resistencia la paso de la corriente eléctrica. |
}} | }} | ||
| + | '''Impedancia eléctrica'''. Cuando en un circuito de [[corriente alterna]] en el que se encuentran conectados, [[Resistencia eléctrica|resistencias]], [[condensadores]] y [[bobinas]], circula una [[corriente eléctrica]], surge una oposición al paso de dicha corriente denominada impedancia. | ||
| + | == Cálculo de la impedancia eléctrica == | ||
| − | + | La impedancia tiene unidades de [[Ohmios]] (Ohms). Y es la suma de una componente resistiva (debido a las resistencias) y una componente reactiva (debido a las bobinas y los condensadores) | |
| − | |||
| − | |||
| − | |||
| − | La impedancia tiene unidades de Ohmios (Ohms). Y es la suma de una componente resistiva (debido a las resistencias) y una componente reactiva (debido a las bobinas y los condensadores) | ||
| − | |||
| + | [[Image:Z.png|100px|]] | ||
donde: | donde: | ||
| − | + | ||
| − | + | Z es la impedancia en Ω | |
| − | X reactancia en Ω | + | |
| + | R es la resistencia en Ω | ||
| + | |||
| + | X es la reactancia en Ω | ||
| + | |||
La impedancia También puede representarse como la suma de una parte real y una parte imaginaria: | La impedancia También puede representarse como la suma de una parte real y una parte imaginaria: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Z=R+jX | |
| + | |||
| + | R es la parte resistiva o real de la impedancia y X es la parte [[reactiva]] o imaginaria de la impedancia. Básicamente hay dos clases o tipos de reactancias: | ||
| + | [[Reactancia inductiva]] XL : Debida a la existencia de [[inductores]]. | ||
| + | [[Reactancia capacitiva]] XC: Debida a la existencia de [[capacitores]]. | ||
| + | == Impedancia en series y paralelo == | ||
| + | |||
| + | Las impedancias se tratan como las [[Resistencia eléctrica|resistencias]] con la [[ley de Ohm]]. La impedancia es igual a su suma: | ||
| + | |||
| + | Serie | ||
| + | |||
| + | [[Image:Z1.png|150px|]] | ||
| + | |||
La impedancia de varias impedancias en paralelo es igual al inverso de la suma de los inversos: | La impedancia de varias impedancias en paralelo es igual al inverso de la suma de los inversos: | ||
| − | Paralelo | + | |
| + | Paralelo | ||
| + | |||
| + | [[Image:Z2.png|150px|]] | ||
| + | |||
== Representación gráfica == | == Representación gráfica == | ||
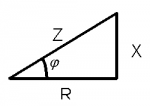
| − | Se puede demostrar que los tres componentes (R, X, Z) se relacionan mediante un triángulo rectángulo. Aplicando el Tª de Pitágoras o relaciones trigonométricas, se pueden obtener muchas más fórmula que relacionen R, X y Z. | + | Se puede demostrar que los tres componentes (R, X, Z) se relacionan mediante un triángulo rectángulo. Aplicando el Tª de [[Pitágoras]] o relaciones trigonométricas, se pueden obtener muchas más fórmula que relacionen R, X y Z. |
| − | |||
| + | [[Image:Z5.png|150px|]] [[Image:Z4.png|150px|]] | ||
| − | + | == Fuentes == | |
| − | |||
| + | * Análisis de los circuitos de Corriente Alterna. [http://www.cifp-mantenimiento.es/e-learning/index.php?id=1&id_sec=7 Concepto de impedancia (Z)]. Consultado: 4 de junio de 2013. | ||
| + | * [http://es.wikipedia.org/wiki/Impedancia Impedancia]. Consultado: 4 de junio de 2013. | ||
[[Category:Magnitudes físicas]] [[Category:Tecnología_electrónica]] | [[Category:Magnitudes físicas]] [[Category:Tecnología_electrónica]] | ||
última versión al 00:17 23 ago 2019
| ||||||
Impedancia eléctrica. Cuando en un circuito de corriente alterna en el que se encuentran conectados, resistencias, condensadores y bobinas, circula una corriente eléctrica, surge una oposición al paso de dicha corriente denominada impedancia.
Sumario
Cálculo de la impedancia eléctrica
La impedancia tiene unidades de Ohmios (Ohms). Y es la suma de una componente resistiva (debido a las resistencias) y una componente reactiva (debido a las bobinas y los condensadores)
donde:
Z es la impedancia en Ω
R es la resistencia en Ω
X es la reactancia en Ω
La impedancia También puede representarse como la suma de una parte real y una parte imaginaria:
Z=R+jX
R es la parte resistiva o real de la impedancia y X es la parte reactiva o imaginaria de la impedancia. Básicamente hay dos clases o tipos de reactancias: Reactancia inductiva XL : Debida a la existencia de inductores. Reactancia capacitiva XC: Debida a la existencia de capacitores.
Impedancia en series y paralelo
Las impedancias se tratan como las resistencias con la ley de Ohm. La impedancia es igual a su suma:
Serie
La impedancia de varias impedancias en paralelo es igual al inverso de la suma de los inversos:
Paralelo
Representación gráfica
Se puede demostrar que los tres componentes (R, X, Z) se relacionan mediante un triángulo rectángulo. Aplicando el Tª de Pitágoras o relaciones trigonométricas, se pueden obtener muchas más fórmula que relacionen R, X y Z.
Fuentes
- Análisis de los circuitos de Corriente Alterna. Concepto de impedancia (Z). Consultado: 4 de junio de 2013.
- Impedancia. Consultado: 4 de junio de 2013.