Diferencia entre revisiones de «Función Cúbica»
| Línea 14: | Línea 14: | ||
[[Image:Gráfica de la función cúbica.JPG]] | [[Image:Gráfica de la función cúbica.JPG]] | ||
| − | + | == Propiedades == | |
*El dominio de la función es la recta real es decir (-α : α) | *El dominio de la función es la recta real es decir (-α : α) | ||
*El recorrido de la función es decir la imagen es la recta real. | *El recorrido de la función es decir la imagen es la recta real. | ||
| Línea 24: | Línea 24: | ||
*La función puede tener hasta un máximo de 3 puntos de intersección con el eje X. | *La función puede tener hasta un máximo de 3 puntos de intersección con el eje X. | ||
| − | + | == Ejemplos == | |
Grafique y analice las propiedades de la siguientes funciones. | Grafique y analice las propiedades de la siguientes funciones. | ||
a) f(x) = 2x<sup>3</sup> + 3x<sup>2</sup> - 12x | a) f(x) = 2x<sup>3</sup> + 3x<sup>2</sup> - 12x | ||
| Línea 39: | Línea 39: | ||
Para demostrar la simetría analíticamente de selecciona un número cualesquiera y su opuesto ejemplo 1 y -1 | Para demostrar la simetría analíticamente de selecciona un número cualesquiera y su opuesto ejemplo 1 y -1 | ||
Demostrar que f(-1) = - f(1). | Demostrar que f(-1) = - f(1). | ||
| − | + | f(-1) = 2(-1)<sup>3</sup> + 12 . (-1)<sup>2</sup> + 2. (-1 ) | |
| − | + | = 2.(-1) + 12 . 1 - 2. | |
| − | + | = -2 + 12 - 2 | |
| − | + | = 10 - 2 | |
| − | + | = 8 | |
| − | + | f(1) = 2(1)<sup>3</sup> + 12 . (1)<sup>2</sup> + 2. (1 ) | |
| − | + | = 2.(1) - 12 . 1 + 2 | |
| − | + | = 2 - 12 + 2 | |
| − | + | = -10 + 2 | |
| − | + | = -8 | |
| − | + | Como f(-1) = - f(1) por tanto la función es simétrica. | |
*Continuidad: La función es continua en todo su dominio pues gráficamente se puede observar que no tiene ningún punto de discontinuidad. | *Continuidad: La función es continua en todo su dominio pues gráficamente se puede observar que no tiene ningún punto de discontinuidad. | ||
*La función no tiene asuntotas. | *La función no tiene asuntotas. | ||
| − | * Para determinar los puntos donde la función corta el eje de la y | + | *Para determinar los puntos donde la función corta el eje de la y |
Se determina el valor de la función para x=0 | Se determina el valor de la función para x=0 | ||
| − | + | f(0) = 2. 0<sup>3</sup> + 3. 0<sup>2</sup> - 12. .0 | |
Obteniendo y= 0 y la función corta el eje de la y en el punto (0:0) | Obteniendo y= 0 y la función corta el eje de la y en el punto (0:0) | ||
Revisión del 13:42 11 jul 2011
| ||||
Función Cúbica. La función Cúbica es generalmente utilizada para relacionar volúmenes en determinados espacio o tiempo. Otro ejemplo es el relacionar el crecimiento de un feto en gestación con el hecho de relacionar su distancia de los pies a la cabeza se puede determinar la semanas de gestación del feto. También el hecho de relacionar los vientos o la energía eólica con respecto a la intensidad de estos y su tiempo de duración. Se utiliza más en el campo de la economía y de la física.
Sumario
Definición
La función cúbica se define como el polinomio de tercer grado; el cual se expresa de la forma: f(x) = ax3 + bx2 + cx + d con a ≠ 0, a, b, c y d Œ IR
Función Cúbica
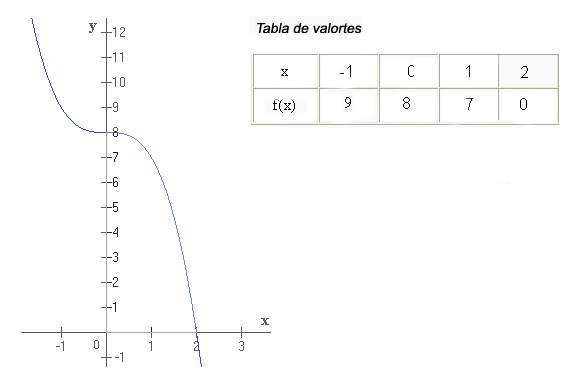
Un ejemplo de función cúbica es: y = f(x) = x3, es la llamada: parábola cúbica.

Propiedades
- El dominio de la función es la recta real es decir (-α : α)
- El recorrido de la función es decir la imagen es la recta real.
- La función es simétrica respecto del origen, ya que f(-x)=-f(x).
- La función es continua en todo su dominio.
- La función es siempre creciente.
- La función no tiene asintotas.
- La función tiene un punto de corte con el eje Y.
- La función puede tener hasta un máximo de 3 puntos de intersección con el eje X.
Ejemplos
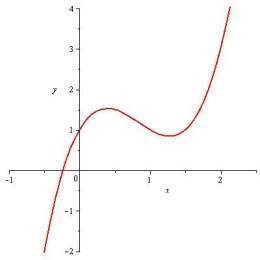
Grafique y analice las propiedades de la siguientes funciones. a) f(x) = 2x3 + 3x2 - 12x Archivo:Ejercicio 1a.jpg Propidades
- Dominio: El conjunto de los Reales
- Imagen: El conjunto de los Reales
- Ceros de la función:
Se iguala la función a cero 2x3 + 3x2 - 12x = 0 x( 2x2 + 3x - 12) = 0 Extrayendo factor común
x = 0 ( 2x2 + 3x + 12)= 0 Igualando a cero ambos factores y realizar la descomposición
- Simetría: Demostrar que cumple f(-x)=-f(x).
Para demostrar la simetría analíticamente de selecciona un número cualesquiera y su opuesto ejemplo 1 y -1 Demostrar que f(-1) = - f(1). f(-1) = 2(-1)3 + 12 . (-1)2 + 2. (-1 )
= 2.(-1) + 12 . 1 - 2.
= -2 + 12 - 2
= 10 - 2
= 8
f(1) = 2(1)3 + 12 . (1)2 + 2. (1 )
= 2.(1) - 12 . 1 + 2
= 2 - 12 + 2
= -10 + 2
= -8
Como f(-1) = - f(1) por tanto la función es simétrica.
- Continuidad: La función es continua en todo su dominio pues gráficamente se puede observar que no tiene ningún punto de discontinuidad.
- La función no tiene asuntotas.
- Para determinar los puntos donde la función corta el eje de la y
Se determina el valor de la función para x=0 f(0) = 2. 03 + 3. 02 - 12. .0 Obteniendo y= 0 y la función corta el eje de la y en el punto (0:0)
EJERCICIOS
Grafique y analice las siguientes funciones cúbicas. 1) f(x) = x3 + 12x + 2 2) f(x) = x3 + 3x2 + 9x 3) f(x) = 3x2 + x3 - 1
Enlaces relacionado
Véase también
- Funciones lineales.
- Funciones cuadráticas.
- Funciones trigonométricas
- Funciones exponenciales
- Funciones logarítmicas.
- Funciones potenciales.
Fuente
- Colectivo de autores. Matemática 8vo grado. Editorial Pueblo y Educación. 1990.
- Libro de texto Matemática 10mo grado. Editorial Pueblo y Educación. 1990.
- Cuaderno Complementario. Matemática 9 no grado. Editorial Pueblo y Educación. 2005.