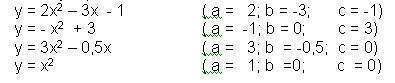Función Cuadrática
| ||||||
Función Cuadrática . Es la correspondencia que a cada X € R le hace corresponder el numero real f (x) = a x ² + b x + c, donde a, b y c son números reales dados.
Sumario
Función f (x) = a x ² + b x + c
En general, el gráfico de una función cuadrática f (x) = a x ² + b x + c es una parábola cuyo eje de simetría es la recta perpendicular al eje x que contiene al vértice, que es el punto del gráfico que tiene el menor (mayor) valor de las imágenes, y esta abre hacia arriba si a > 0 y hacia abajo si a < 0.
Los valores a, b y c pertenecientes a los reales y a ≠ 0.
Ejemplos de funciones cuadráticas
En ocasiones para enfrentar una situación en particular en nuestro diario vivir, se hace necesaria la utilización de funciones cuadráticas para dar respuestas a inquietudes como las dimensiones de un terreno, la altura alcanzada por cierto objeto o el tiempo de recorrido de este objeto. Veamos algunos casos a manera de ejemplo. Son ejemplos de funciones cuadráticas:
Dominio de la Función f (x) = a x ² + b x + c
Los elementos del dominio de la Función cuadrática f (x) = a x ² + b x + c (a ≠ 0) cuyas imágenes forman un valor cero, se denomina ceros de esta función. La existencia de los ceros de una función cuadrática depende del valor del discriminante D = b ² - 4ac de la ecuación de segundo grado que la define.
Simetría
Sea f (x) = ax2 +bx +c el criterio de una función cuadrática, el eje de simetría de una parábola es la recta vertical de ecuación
Esta recta es importante cuando se realiza la gráfica de una función cuadrática, pues divide a la parábola en dos partes congruentes, es decir, cualquier punto de la parábola tendrá un punto homólogo al otro lado de este eje.
Cuando el coeficiente b= 0, entonces el eje de simetría es la recta vertical de ecuación x =0, es decir el eje “y”, decimos entonces que la parábola tiene una simetría Par.
Monotonía de la función cuadrática
Recordar que:
1. Si f '(a) > 0 entonces f es creciente en “a”.
2. Si f '(x) < 0 entonces f es decreciente en “a”.
3. Si f '(x) = 0 y f´´(a)≠0 entonces se dice que f tiene un valor extremo en a.
La representación de las funciones cuadráticas es una parábola con eje de simetría paralelo al eje de ordenadas, que la divide en dos ramas, una creciente y otra decreciente
Vértice
El vértice se constituye en el punto más importante de la parábola por la cantidad de propiedades que define para la misma. Las coordenadas de dicho punto determinan el eje de simetría de la gráfica, la monotonía de la función, su imagen o recorrido. Analizaremos dos formas de encontrar el par ordenado (Xv;Yv)
Representación gráfica
Para representar gráficamente una función f cualquiera te proponemos seguir el procedimiento siguiente.
- Calcular los ceros si los posee.
- Calcular las coordenadas del vértice.
- Calcular algunos puntos y sus simétricos respecto al eje de la parábola.
- Representar los puntos determinados, en un sistema de coordenadas rectangulares.
- Unir los puntos representados mediante una parábola.