Integral Indefinida

Integral indefinida Concepto: El campo vectorial definido asignando a cada punto (x, y) un vector que tiene por pendiente ƒ(x) = (x3/3)-(x2/2)-x. Se muestran tres de las infinitas primitivas de ƒ(x) que se pueden obtener variando la constante de integración C.

Integral indefinida. Es el conjunto de las infinitas primitivas que puede tener una función.

Definición

Integrar es el proceso recíproco del de derivar, es decir, dada una función f(x), busca aquellas funciones F(x) que al ser derivadas conducen a f(x).

Se dice, entonces, que F(x) es una primitiva o antiderivada de f(x); dicho de otro modo las primitivas de f(x) son las funciones derivables F(x) tales que:

F'(x) = f(x).

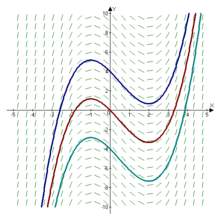
Si una función f(x) tiene primitiva, tiene infinitas primitivas, diferenciándose todas ellas en una constante.

[F(x) + C]' = F'(x) + 0 = F'(x) = f(x)

Integral indefinida

Integral indefinida es el conjunto de las infinitas primitivas que puede tener una función.

Se representa por ∫ f(x) dx.

Se lee como "la integral indefinida de f(x) respecto a x" Por lo tanto, f(x) dx es una conjunto de funciones; no es una función sola, ni un número.

La función f que se está integrando se llama el integrando, y la variable x se llama la variable de integración.

C es la constante de integración y puede tomar cualquier valor numérico real.

Si F(x) es una primitiva de f(x) se tiene que:

∫ f(x) dx = F(x) + C

Para comprobar que la primitiva de una función es correcta basta con derivar.

Integrales inmediatas

Si u = x (u' = 1), tenemos una tabla de integrales simples:

• 

• 

• 

• 

• 

• ∫ cos x dx = sen x + C

• 

• 

• 

• 

Propiedades

1. La integral del producto de una constante por una función es igual a la constante por la integral de la función.

∫ k f(x) dx = k ∫f(x) dx

2. La integral de una suma de funciones es igual a la suma de las integrales de esas funciones.

∫[f(x) + g(x)] dx =∫ f(x) dx +∫ g(x) dx

Ejemplos

• 

• 

Métodos de integración

Existen varios métodos entre los que se destacan los siguientes:

• Integración por Cambio de variable.
• Integración por partes para integrar productos de funciones.
• Integración de funciones trigonométricas.
• Integración de funciones racionales..

Vea también

• Integración numérica

• Integral Definida

• Derivada de una función

Fuentes

• Integral indefinida [citado 2011 agosto, 8]; Disponible en:http://www.vitutor.com/integrales/indefinidas/integral_indefinida.html

• Integrales inmediatas [citado 2011 agosto, 8]; Disponible en:http://es.wikipedia.org/wiki/Integraci%C3%B3n_indefinida