Función
| ||||||
Función. Este concepto está implícito en las Matemáticas desde las primeras civilizaciones, con el estudio de las tablillas de barro babilónicas de la colección de Plimpton, que datan del año 1900 a.n.e. Este se conserva a lo largo de la historia de la matemática, Descartes (1596-1652) muestra que tiene la idea intuitiva de variable y función. Sin embargo, la palabra función no surge hasta que el matemático alemán W.G. Leibniz (1646-1652) la utiliza en 1694 para designar la dependencia entre los valores de las abscisas y los puntos de la representación gráfica.
Hablando del concepto de fúnción: "Lo encontramos utilizado con nombres diversos en todas las matemáticas contemporáneas: aplicación, homomorfismo, transformación, correspondencia, interpretación, representación, operador, funtor, mapeo, etc. " Mauricio Loi
Sumario
Definición
Una función es una correspondencia que a cada elemento de un conjunto A asocia un único elemento de un conjunto B.
Un conjunto de pares ordenados (x ; y) tales que x € A, y y € B es una función o aplicación de A en B, si a cada elemento x € A le corresponde un único elemento y € B.
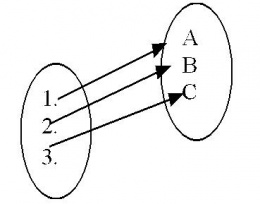
- Visión sagital
Estamos en presencia de una función cuando de cada elemento del primer conjunto sale una única flecha hacia un elemento del segundo conjunto; sin embargo, hacia un elemento del segundo pueden llegar más de una flecha.
Algunas propiedades de las funciones
- Al conjunto A se denomina dominio y sus elementos se les llaman argumentos o preimágenes.
- A los elementos de B que son correspondientes de algún elemento de A se les llama imágenes, y el conjunto de ellos se denomina conjunto imagen de la función.
- Si f es una función y x0 es un elemento del dominio de f, la imagen del argumento x0 se denota f (x0).
- El elemento del dominio cuya imagen es cero, se denomina cero de la función (Una función puede tener un cero, varios ceros o no tener ceros)
- Una función es inyectiva si para dos valores iguales de la imagen le corresponden valores iguales del dominio.
- Una función es biyectiva si a cada elemento de y le corresponde un único elemento de x.
- Una función es par si f( x ) = f( - x )
- Una función es impar si f( x ) = - f( x)
- Una función es creciente (decreciente) en un intervalo [a,b] si al tomar dos puntos cualesquiera del mismo, x1 y x2, con la condición x1 < x2, (x1 > x2) se verifica que: f(x1 ) < f(x2 ). ( f(x1 ) > f(x2 ))
Formas de representar las funciones
La ley de formación para obtener los pares ordenados (x ; y) de una función se puede expresar de diferentes formas:
- Mediante una descripción oral.
- Mediante una tabla de valores.
- Mediante una representación gráfica.
- Mediante una ecuación.
Ejemplos de las formas de representar funciones
- A cada instante del día se le hace corresponder una determinada temperatura.
- La siguiente tabla representa la dependencia entre un número entero y su cuadrado
| x |
-2 |
-1 |
0 |
1 |
2 |
| x2 |
4 |
1 |
0 |
1 |
4 |
3. Mediante una representación grafica.
4. f(x) = 4 x + 5
Algunos tipos de funciones
- Funciones lineales.
- Funciones cuadráticas.
- Función Cúbica
- Funciones trigonométricas
- Función exponencial
- Funciones logarítmicas.
- Funciones potenciales.
Véase también
- Funciones lineales.
- Funciones cuadráticas.
- Funciones trigonométricas
- Funciones exponenciales
- Funciones logarítmicas.
- Funciones potenciales.
Fuentes
- Colectivo de autores. Matemática 8vo grado. Editorial Pueblo y Educación. 1990.
- Libro de texto Matemática 10mo grado. Editorial Pueblo y Educación. 1990.
- Cuaderno Complementario. Matemática 9 no grado. Editorial Pueblo y Educación. 2005.