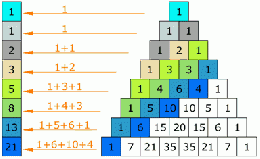
Números de Fibonacci
| ||||
Números de Fibonacci Una sucesión de números muy conocida y usada en matemáticas es, precisamente, la sucesión de Fibonacci. Leonardo de Pisa, más conocido como Fibonacci construyó por primera vez la sucesión que lleva su nombre.
Definición
Se llaman números de Fibonacci a aquellos que forman parte de la sucesión infinita de numeros naturales donde cada número se calcula sumando los dos anteriores a él.
La sucesión de Fibonacci es la sucesión de números:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 88, 144, ...
Historia
La sucesión de Fibonacci es una secuencia de números enteros descubierta por matemáticos hindúes hacia el año 1135 y descrita por primera vez en Europa gracias a Leonardo Fibonacci.
Esta sucesión fue descrita por Fibonacci como la solución a un problema de la cría de conejos.
Muchas propiedades de la sucesión de Fibonacci fueron descubiertas por Édouard Lucas, responsable de haberla denominado como se la conoce en la actualidad.
Esta serie ha tenido popularidad en el siglo XX especialmente en el ámbito musical, en el que compositores como Béla Bartok u Olivier Messiaen la han utilizado para la creación de acordes y de nuevas estructuras de frases musicales.
Regla
La sucesión de Fibonacci se puede escribir como una "regla": la regla es xn = xn-1 + xn-2 donde: xn es el término en posición "n" xn-1 es el término anterior (n-1) xn-2 es el anterior a ese (n-2) Por ejemplo el sexto término se calcularía así:
x6 = x6-1 + x6-2 = x5 + x4 = 5 + 3 = 8.
Propiedades curiosas
La sucesión de Fibonacci tiene muchas propiedades curiosas:
- La suma de los n primeros términos es: a1 + a2 +... + an = an+2 - 1
- La suma de los términos impares es: a1 + a3 +... + a2n-1 = a2n
- La suma de los términos pares es: a1 + a4 +... + a2n = a2n+1 - 1
- La suma de los cuadrados de los n primeros términos es: a12 + a22 +... + an2 = anan+1
- Si n es divisible por m entonces an es divisible por am
- Los números consecutivos de Fibonacci son primos entre si.
- La propiedad mas curiosa de esta sucesión es que el cociente de dos números consecutivos de la serie se aproxima a la razón áurea. Esto es: an+1/an tiende a (1 + ð 5)/2
Aplicaciones
Las aplicaciones de esta sucesión en nuestra vida diaria son:
- La mano humana.
- El número de pétalos de una flor.
- Las espirales de los girasoles.
- Las espirales de las piñas.
- La altura de la cadera y la altura de la rodilla.
- La altura de un ser humano y la altura de su ombligo.
- La cría de los conejos.
- La mona lisa
Y muchas otras cosas…