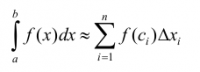Integración numérica

Integración numérica Concepto: Se aplica en las diferentes ramas de la Geometría, la Física, la Química, las Ciencias Económicas y, prácticamente, en todas las ramas del saber.

Integración numérica. En las matemáticas el estudio de las integrales es fundamental ya que resuelve muchos problemas de la vida diaria, esta rama se estudia en el Cálculo Infinitesimal como integral definida función f(x) en un intervalo [a, b] como el resultado de un proceso de límite de una suma finita.

Aplicaciones en las diferentes ramas

El lector seguramente recuerda las importantes aplicaciones que poseen las integrales en las diferentes ramas de la Geometría, la Física, la Química, las Ciencias Económicas y, prácticamente, en todas las ramas del saber. Supuesto que f(x) sea continua en [a, b], la integral se puede calcular mediante la regla de Barrow (también llamada de Newton – Leibniz), donde F(x) es cualquier primitiva de f(x), es decir, una función cuya derivada de una función sea f(x).

El punto débil de este procedimiento analítico para evaluar una integral es la obtención de una función primitiva. Para muchas funciones sencillas se obtienen primitivas con mayor o menor dificultad pero, en muchos casos se presentan integrales para las cuales no existen primitivas que se puedan expresar en términos de funciones elementales.

Lo peor es que, en muchas ocasiones, se trata de integrandos sencillos (es decir, formados por funciones elementales). Por supuesto que, si no se tiene una primitiva expresada en términos de funciones elementales, no es posible evaluarla en los límites de integración, y la regla de Barrow se hace inaplicable.

Método de los trapecios

Aunque el método más elemental para calcular la integral definida de una función consiste en utilizar la misma definición de la integral definida pero prescindiendo del proceso de límite de una función, es decir:

el resultado que se obtiene es muy inexacto, a menos que se tome un número n de subintervalos muy grande. El método de los trapecios que se expone a continuación requiere una cantidad de cálculos semejante a la expresión (1) y produce resultados mucho mejores.

El método de los trapecios se basa en la idea de dividir el intervalo de integración en n subintervalos de amplitud h mediante un conjunto de puntos {a = x0, x1, x2, ..., xn = b} y descomponer la integral en n integrales, cada una de las cuales posee un intervalo de integración pequeño de longitud h, como se ilustra en la figura. El parámetro h se denomina paso y juega un papel importante en la exactitud del resultado obtenido.

Método de Simpson

El metodo de Simpson es una mejora al de los trapecios ya que la aproximación se realiza con Polinomio interpoladores de grado dos. Considérese la integral:

donde se supondrá que f(x) es continua en [a, b]. Sea el intervalo de integración dividido en un número par de intervalos de igual amplitud h mediante los puntos {a = x0, x1, x2, ..., xn = b}. Las figuras 1 y 2 muestran la idea geométrica del método de Simpson: en la figura 1 se aprecia que la región comprendida entre el eje horizontal y la gráfica de f(x) se ha dividido en franjas verticales mediante rectas que determinan los puntos de la partición de [a, b]. En la figura 2 se ha sustituido la función f(x) por un conjunto de polinomios de grado 2, es decir, parábolas de eje vertical.

Al igual que en el método de los trapecios, la notación se simplificará llamando yi = f(xi) para i = 0, 1, 2,..., n.

Fuente

• Álvarez, Manuel, Alfredo Guerra y Rogelio Lau. Matemática numérica, 2da Edición.