Logaritmo

Logaritmo Concepto: Logaritmo de un número –en una base determinada– es el exponente al cual hay que elevar la base para obtener dicho número. Es la función matemática inversa de la función exponencial

Logaritmo.Los logaritmos fueron introducidos en las matemáticas con el propósito de facilitar, simplificar o incluso, hacer posible complicados cálculos numéricos. Utilizando logaritmos podemos convertir: productos en sumas, cocientes en restas, potencias en productos y raíces en cocientes.

A las operaciones, ya conocidas, de Adición, Sustracción, Multiplicación, División, Potenciación y Radicación, añadimos una nueva que llamamos Logaritmación.

Historia

Motivación

La invención de los logaritmos surge como respuesta a motivaciones económicas y culturales:

• La motivación cultural es el avance en el estudio de la astronomía, basada en la trigonometría plana y esférica , se realizaba con cálculos arduos y tediosos. Había que simplificar, con recursos operatorios más rápidos.
• La motivación económica . Luego del surgimiento del capitalismo y la invasión de América, se lleva la riqueza saqueada a Europa. Había que contar con una navegación más eficiente y segura. Rumbo preciso, posible ubicación del barco en altamar, requiere mejorar los cálculos trigonométricos.
• Otra motivación económica, el capital-surgido con el oro y plata del Nuevo Mundo- controlado por la Banca y sometido a finanzas gana intereses: surgen expresiones del tipo de Cx1.05⁸, en 8 años; que al variar el tiempo, para 5 años y 6 meses se trataría de calcular Cx1.05^5.5 el interés compuesto de un capital C, a un 5% de interés anual durante 5 años y 6 meses.

Estas circunstancias de desarrollo social económico acuciaron cálculos más rápidos y potentes y atacar nuevos casos. Se resuelven estos problemas con la creación de logaritmos, que significó un cambio dialéctico respecto a los cálculos anteriores.

El método de cálculo mediante logaritmos fue propuesto por primera vez, públicamente, por John Napier (latinizado Neperus) en 1614, en su libro titulado Mirifici Logarithmorum Canonis Descriptio. Joost Bürgi, un matemático y relojero suizo al servicio del duque de Hesse-Kassel, concibió por primera vez los logaritmos, sin embargo, publicó su descubrimiento cuatro años después que Napier. La inicial resistencia a la utilización de logaritmos fue cambiada por Kepler, por el entusiasta apoyo de su publicación y la impecable y clara explicación de cómo funcionaban. Este método contribuyó al avance de la ciencia, y especialmente de la astronomía, facilitando la resolución de cálculos muy complejos. Los logaritmos fueron utilizados habitualmente en geodesia, navegación marítima y otras ramas de la matemática aplicada, antes de la llegada de las calculadoras y computadoras. Además de la utilidad en el cálculo, los logaritmos también ocuparon un importante lugar en las matemáticas más avanzadas; el logaritmo natural presenta una solución para el problema de la cuadratura de un sector hiperbólico ideado por Gregoire de Saint-Vincent en 1647.

Napier no usó una base tal como ahora se entiende pero, sus logaritmos, como factor de escala, funcionaban de manera eficaz con base 1/e. Para los propósitos de interpolación y facilidad de cálculo, eran útiles para hallar la relación r en una serie geométrica tendente a 1. Napier escogió r = 1 - 10−7 = 0,999999 (Bürgi eligió r = 1 + 10−4 = 1,0001). Los logaritmos originales de Napier no tenían log 1 = 0, sino log 107 = 0. Así, si N es un número y L es el logaritmo, Napier calcula: N = 107(1 − 10−7)L. Donde (1 − 10−7)107 es aproximadamente 1/e, haciendo L/107 equivalente a log1/e N/107.

Inicialmente, Napier llamó "números artificiales" a los logaritmos y "números naturales" a los antilogaritmos. Más tarde, Napier usa la palabra logaritmo en el sentido de un número que indica una proporción: λόγος (logos) el sentido de proporción, y ἀριθμός (arithmos) significado número, y se define, literalmente, como «un número que indica una relación o proporción». Se refiere a la proposición que fue hecha por Napier en su "teorema fundamental", que establece que la diferencia de dos logaritmos determina la relación de los números a los cuales corresponden, de manera que una progresión aritmética de logaritmos corresponde a una progresión geométrica de números. El término antilogaritmo fue introducido a finales de siglo XVII y, aunque nunca se utilizó ampliamente en matemáticas, perduró en muchas tablas, hasta que cayó en desuso.

Definición

Dado dos números reales a y b (a>0, a ≠1 y b>0) se cumple que:  Archivo:Definición de logaritmo.JPG Y se lee "el logaritmo en base a del número b es c" entonces a elevado a la C se obtiene b.

Ejemplos

Determina los siguientes logaritmos: Archivo:Ejemp definición.JPG

Ejercicios Resueltos

Determina en cada caso el valor de y.

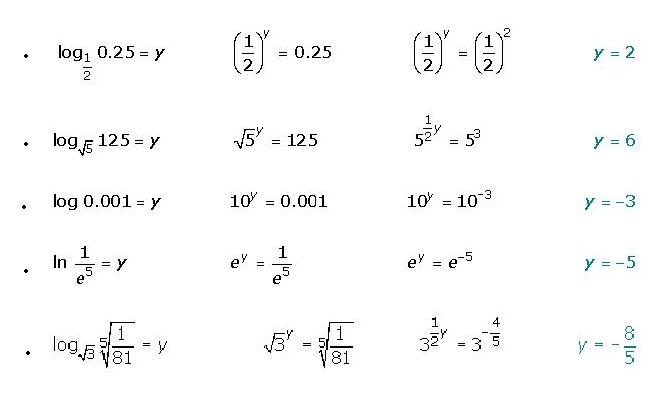
Propiedades

- El logaritmo de un producto es igual a la suma de los logaritmos de los factores.

- El logaritmo de un cociente es igual al logaritmo del numerador menos el logaritmo del denominador.

- El logaritmo de una potencia es igual al producto entre el exponente y el logaritmo de la base de la potencia.

- El logaritmo de una raíz es igual al logaritmo del radicando dividido por el índice

Propiedades respecto a una relación de orden

• Función creciente: si a > 1; O < m < n; entonces log_a m < log_an ; a mayor número mayor logaritmo.
• Función decreciente: si 0 < a < 1, 0 < p <q, entonces log_a p > log_a q; a menor número mayor logaritmo.
• Variación de las bases. 1< a <A, k el número (logaritmando) no varía, entonces log_Ak < log_ak, a mayor base menor logaritmo para el mismo número. Así el log2 = 0.30103, ln2 = 0.69315, el logaritmo vulgar de 2 es menor que su logaritmo natural ; pero la base e = 2.71828... de los logaritmos naturales es menor que la base 10 de los logaritmos vulgares.

Ejemplos

Calcula aplicando las propiedades del logaritmo.

Son comunes los logaritmos en base e (logaritmo neperiano), base 10 (logaritmo común), base 2 (logaritmo binario), o en base indefinida (logaritmo indefinido). La elección de un determinado número como base de los logaritmos no es crucial, ya que todos son proporcionales entre sí. Es útil la siguiente fórmula que define al logaritmo de x en base b (suponiendo que b, x, y k son números reales positivos y que tanto "b" como "k" son diferentes de 1.

Otras propiedades de los logaritmos

Prop.jpg

1.El logaritmo de la base es 1.
2.El logaritmo de 1 es 0, cualquiera que sea la base.
3.Cambio de base: El logaritmo en base a de un número se puede obtener a partir de logaritmos en otra base.
4.

Logaritmos decimales

Son los que tienen base 10. Se representan por log (x).

Los logaritmos decimales tienen, en general, una parte entera y una parte fraccionaria.

- Se denomina característica a la parte entera del logaritmo.

- Se denomina mantisa a la parte fraccionaria (que puede ser cero).

Logarítmos neperianos

Son los que tienen base e. Se representan por ln (x) o L(x).

Bibliografía

Serpa,  Alfredo. Series(2004). Editorial Félix Varela, La Habana.

Véase también

• Series matemáticas
• Matemáticas aplicadas
  
• Matemáticas
• Matemática Discreta
• Monotonía de la Logaritmación
• Progresiones