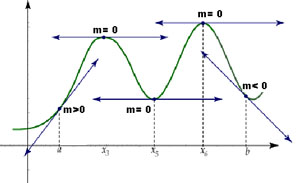
Monotonía de la función cuadrática

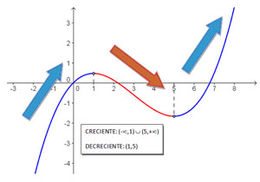
Monotonía de la Función Cuadrática Concepto: Es la propiedad de la función que caracteriza su variación respecto a la variación de la variable independiente x. Comprende los conceptos de crecimiento y decrecimiento.

Monotonía . Puede caracterizarse como el movimiento de nuestros ojos cuando recorremos el gráfico de la función de izquierda a derecha. Su evaluación permite determinar (en la gráfica) puntos conocidos como extremos, donde la función cambia su monotonía, ha dejado de crecer y aun no está decreciendo, o viceversa. .
La monotonía puede analizarse tanto para intervalos como para puntos específicos de una función dada.

Monotonía por intervalos

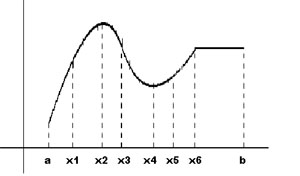
Analizando funciones reales en una variable se pueden definir hasta cinco categorías diferentes. .

Función estrictamente creciente en un intervalo.
1. Se dice que la función es estrictamente creciente en el intervalo (a,b) cuando para todo x1; x2 ∈ (a,b), tal que x1<x2 se cumple que f(x1)<f(x2). Esto significa gráficamente, como se señaló anteriormente, que al avanzar hacia la derecha en él la función solo sube. .
2. Función creciente en un intervalo.
Se dice que la función es creciente en el intervalo (a,b) cuando para todo x1; x2 ∈ (a,b), tal que x1<x2 se cumple que f(x1)≤f(x2). En este caso es necesario señalar que se verifican ambas condiciones (igualdad y crecimiento) a lo largo del intervalo. Esto significa gráficamente, como se señaló anteriormente, que al avanzar hacia la derecha en él la función es constante y sube..
3. Función constante en un intervalo
Se dice que la función es constante en el intervalo (a,b) cuando para todo x1; x2 ∈ (a,b), tal que x1<x2 se cumple que f(x1)=f(x2). Esto significa gráficamente, como se señaló anteriormente, que al avanzar hacia la derecha en él la función es constante. Las funciones de la forma f(x)=k son constantes en todo su dominio.
4. Función decreciente en un intervalo
Se dice que la función es decreciente en el intervalo (a,b) cuando para todo x1; x2 ∈ (a,b), tal que x1<x2 se cumple que f(x1)≥f(x2). En este caso es necesario señalar se verifican ambas condiciones (igualdad y decrecimiento) a lo largo del intervalo. Esto significa gráficamente, como se señaló anteriormente, que al avanzar hacia la derecha en él la función es constante o baja. 5. Función estrictamente decreciente en un intervalo
Se dice que la función es estrictamente de creciente en el intervalo (a,b) cuando para todo x1; x2 ∈ (a,b), tal que x1<x2 se cumple que f(x1)>f(x2). . Esto significa gráficamente, como se señaló anteriormente, que al avanzar hacia la derecha en él la función solo baja. Algunos autores prefieren utilizar para las categorías 2 y 4 los términos ¨no decreciente¨ y ¨no creciente¨, teniendo en cuenta que si la función ¨sube o es constante¨ entonces ¨no decrece¨ mientras que si ¨baja o es constante¨ entonces ¨no crece¨. En esta caso para las categorías 1 y 5 bastaría utilizar los términos creciente y decreciente respectivamente.

Monotonía de funciones en una rama

Para las funciones definidas en una rama es imposible verificar las categorías ¨intermedias¨, es decir la 2 y la 4. Dado un conjunto de pares ordenados (x; f(x)) para todo x∈ R el gráfico puede crecer y decrecer pero no puede ser constante y crecer o decrecer. Para funciones definidas de esta forma es muy práctico el empleo del criterio de monotonía en un punto.
Para analizar la monotonía de la función en un punto dado analizaremos el comportamiento en la vecindad del punto.

Monotonía en un punto

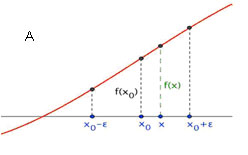
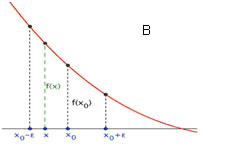
Una función f(x) es creciente en un punto X0 si para todo ε infinitamente pequeño y positivo, se cumple que f(X0-ε)<f(X0)<f(X0+ε), análogamente una función f(x) es decreciente en un punto X0 si para todo ε infinitamente pequeño y positivo, se cumple que f(X0-ε)>f(X0) > f(X0+ε).

Diremos entonces que una función es creciente (decreciente) en el intervalo (a,b) si es creciente (decreciente) para todo x∈ (a,b).
Puntos extremos. Son los puntos más altos y más bajos de la gráfica de una función. En estos puntos dicha función ni crece ni decrece. Pueden ser de dos tipos:

a) Máximo relativo: en un entorno próximo al punto por la izquierda la función crece y en un entorno por la derecha la función decrece, hay un cambio de monotonía de creciente a decreciente: f(x0)>f(x0-) y f(x0)>f(x0+)

b) Mínimo relativo: en un entorno próximo al punto por la izquierda la función decrece y en un entorno por la derecha la función crece, hay un cambio de monotonía de decreciente a decreciente: f(x0)<f(x0-) y f(x0)<f(x0+)

Si el máximo (mínimo) es para toda la función se dice absoluto. Si el máximo (mínimo) es solamente para una zona de la función se dice local.

Monotonía y extremos según criterios de la primera y segunda derivada

Recordar:

1. Si una función es derivable, entonces la primera derivada evaluada en un punto es igual a la pendiente (m) de la recta tangente a la curva en dicho punto.

2. Si el ángulo que forma una recta con el semieje positivo de las abscisas es: 0º entonces la pendiente (m) es igual a 0

Agudo entonces la pendiente (m) es positiva.

Obtuso entonces la pendiente (m) es negativa

Teorema 1:

Sea f una función derivable en el intervalo (a,b).

1. Si f '(x) > 0 para todo x de (a,b), entonces f es creciente en (a,b).

2. Si f '(x) < 0 para todo x de (a,b), entonces f es decreciente en (a,b).

3. Si f '(x) = 0 para todo x de (a,b), entonces f es constante en (a,b).

Teorema 2: Sea f una función con su primera derivada definida, al menos, en un intervalo abierto conteniendo al número a. Si f´´ está definida entonces se cumple:

a).- Si f´(a)=0 y f´´(a)<0 entonces se dice que f tiene un máximo local en a.

b).- Si f´(a)=0 y f´´ (a)>0 entonces se dice que f tiene un mínimo local en a.

Para ver como aplicar los teoremas anteriores, notemos que para f continuas, f '(x) sólo cambia de signo alrededor de sus ceros, luego para determinar los intervalos en que f es creciente o decreciente, sugerimos los siguientes pasos:

• Localizar los interceptos con el eje “x” de la primera derivada de f. (resolviendo la ecuación f '(x) = 0)
• Determinar el signo de f'(x) en un punto de cada intervalo determinado por dos puntos críticos consecutivos.
• Decidir, mediante el Teorema 1, si f es creciente o decreciente en cada uno de esos intervalos.
• Clasificar los puntos extremos mediante el teorema 2.

Significado físico de la monotonía

Al analizar el comportamiento de una magnitud física vectorial (que tiene dirección y sentido) en el tiempo en un sistema de ejes coordenados donde colocamos en el eje de las abscisas el tiempo y en el eje de las ordenadas dicha magnitud física (que llamaremos primaria), la determinación de los intervalos de monotonía y puntos extremos de dicha gráfica nos permite conocer el sentido de otra magnitud física (que llamaremos derivada). Así por ejemplo, en el lanzamiento de proyectiles, la evaluación de la monotonía de una gráfica de altura contra tiempo nos permite conocer el sentido de la velocidad vertical del proyectil; análogamente la evaluación de esta propiedad en una gráfica de carga eléctrica vs tiempo, nos permite caracterizar el sentido de la corriente eléctrica; y en el caso de flujo magnético vs tiempo, a la fuerza electromotriz inducida.

Veamos el primer ejemplo:

La altura en metros de un objeto lanzado desde el suelo hacia arriba después de t segundos está dada por la ecuación h(t) =96t−16t2 .

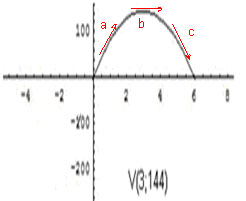
Calculando los ceros de está parábola invertida (0 y 6), conocemos que el tiempo de vuelo es 6 segundos y como la función cuadrática es simétrica respecto a la recta x=xv, la abscisa del vértice es x=3 y su ordenada f(3)= 144. El vértice constituye un máximo global de dicha función. Los intervalos de monotonía son: (0,3) creciente; (3,6) decreciente, en x=3 hay un máximo, por lo tanto la función cambia la monotonía de creciente a decreciente, analicemos el significado físico de la monotonía de h vs t, en la variación instantánea de h, es decir, la componente vertical de la velocidad del objeto. En el tramo (0,3) creciente, vy está dirigida hacia arriba, el objeto está subiendo (figura 4a); en el tramo (3,6) decreciente, vy está dirigida hacia abajo (figura 4c), el objeto está bajando; mientras que en el máximo local, donde no hay cambio de monotonía, vy=0 en este instante de tiempo el objeto ni sube ni baja (figura 4b).

Cálculo de extremos. Problemas de optimización

En ocasiones nos interesa resolver situaciones en las que hay que hallar un valor que haga máximo o mínimo otro, estos problemas se llaman de "optimización". Los problemas de optimización se reducen a obtener los extremos relativos de una función.

Estos problemas a menudo requieren un planteamiento previo que, resumiendo, es el siguiente:

• Determinar la función de la que se quiere obtener el máximo o el mínimo. Es fácil que ésta dependa de más de una variable; en este caso buscar la relación entre ellas para que sólo tengamos una incógnita. • Calcular el máximo o el mínimo pedido, imponiendo las condiciones necesarias en sus derivadas

MÁXIMO f '(x0)=0 y f (x0)<0

MÍNIMO f '(x0)=0 y f (x0)>0

Fuentes

• Brugov, I y S. Nikolski. 1984. Matemáticas superiores. Cálculo diferencial e integral. Editorial Mir Moscú. 405 pp.
• Apostol, T. 1969. Análisis Matemático. Editorial Addison-Wesley. Cuba. 527 pp.
• Colectivo de Autores. 1988. Análisis Matemático I. Facultad de Economía. UH. 437pp.
• Suvorov, I. Curso de Matematicas Superiores. Editorial Mir Moscú. 375 pp.