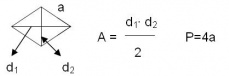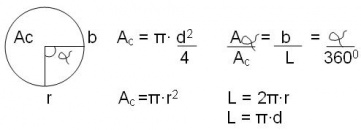Geometría plana
| ||||

Geometría Plana. Etimológicamante, del griego "geo", tierra; "metrein", medir, es la rama de la matemática que se ocupa del estudio de las figuras geométricas en el plano. En general, en su forma elemental y clásica, la geometría se centra en temas métricos como el cálculo del área y perímetro de figuras planas y del área y volumen de cuerpos sólidos. Otros enfoques de la geometría son la geometría analítica, geometría descriptiva, geometría diferencial, topología, geometría del espacio, con cuatro o más dimensiones, geometría fractal, geometrías no euclídeas.
También conocida como Geometría Euclidiana pues el conjunto de propiedades y relaciones sobre las figuras geométricas las expuso el matemático griego Euclides de Alejandría (alrededor del 300 a.n.e.) en su obra magna “Elementos de Geometría”. Obra que resultó abarcadora en su contenido y su estructuración interna tan avanzada para la época que durante siglos se consideró el más completo modelo de exposición de una teoría por vía deductiva. Aunque muchos de los resultados que se exponen en la obra eran ya conocidos, el riguroso orden lógico en la exposición, así como la claridad y estructura lógica de las demostraciones, hacen de esta obra un resultado superior a cuantos se habían escrito antes.
Sumario
Reseña Histórica de la Geometría
La geometría surgió hace miles de años. Muchos consideran que fue la necesidad de medir las tierras la que dio origen a esta parte de la Matemática. Las antiguas civilizaciones construyeron sus viviendas y sus tumbas, sus graneros y canales, edificaron y adornaron sus templos, sus museos y observatorios. De los egipcios se sabe que conocían la construcción de figuras, utilizaban instrumentos geométricos elementales (regla graduadas y compases), construidos por ellos mismos.
La geometría fue introducida en Grecia por uno de los llamados “siete sabios de la Antigüedad” Tales de Mileto, en el siglo VI a.n.e. En el siglo Vll se dieron los primeros pasos en la modernización de la geometría, se introdujo la geometría analítica y algunos de sus principios más elementales como el trabajo con coordenadas. Luego en el siglo XIV le dieron un gran impulso al desarrollo de la misma. El origen del término geometría es una descripción precisa del trabajo de los primeros geómetras, que se interesaban en problemas como la medida del tamaño de los campos o el trazado de ángulos rectos para los esquemas de los edificios. Este tipo de geometría empírica, que floreció en el Antiguo Egipto, Sumeria y Babilonia, fue refinado y sistematizado por los griegos.
En el siglo VI a.n.e. el matemático Pitágoras colocó la piedra angular de la geometría científica al demostrar las diversas leyes arbitrarias e inconexas de la geometría empírica se puede deducir como conclusiones lógicas de un número limitado de acciones, o postulados. Estos postulados fueron considerados por Pitágoras y sus discípulos, como verdades evidentes; sin embargo, en el pensamiento matemático moderno se considera como un conjunto de supuestas útiles pero arbitrarias.
La geometría demostrativa de los griegos se ocupaba de polígonos, círculos y de sus correspondientes, según dice el matemático griego Euclides, en su libro “Los elementos”. El texto de Euclides, a pesar de sus imperfecciones, ha servido como libro de texto básico, hasta la actualidad
El siguiente paso importante en esta ciencia lo dio el filósofo y matemático francés René Descartes, con el discurso del método publicado en 1637. Este trabajo fraguó una conexión entre la geometría y el álgebra al demostrar como aplicar los métodos de una disciplina en otra. Esto es un fundamento de la geometría analítica donde las figuras se representan mediante expresiones algebraicas, sujeto subyugante en la mayor parte de la geometría moderna. Otro desarrollo importante del siglo XVII fue la investigación de las propiedades de las figuras geométricas que no varían cuando las figuras son proyectadas de un plano a otro.
La geometría sufrió un cambio radical de dirección en el siglo XIX. Los matemáticos Carl Friedrich Gauss, Nikolai Labachewski, y János Bayai, trabajaron por separado sistema de coherentes de geometría no euclídea. Este sistema aparece a partir de los trabajos llamados “postulados paralelos” de Euclides al proponer alternativas que generan modelos extraños y no intuitivos de espacio, aunque, eso si, coherentes. El matemático británico Arthuer Cay desarrolló la geometría para espacios con más de tres dimensiones. También se han utilizado métodos analíticos para estudiar las figuras geométricas regulares en cuatro o más dimensiones y compararlos con figuras similares en tres o menos dimensiones, esta se conoce como geometría estructural. Otro concepto dimensional es el de dimensiones fraccionarias, aparecido en el siglo XIX. En la década de 1970 el concepto se desarrolló como la geometría fractal.
¿Para qué sirve la geometría?
De forma general la enseñanza de la Geometría tiene como objetivo genérico desarrollar el pensamiento espacial del ser humano, de modo tal que este pueda hacer una mejor interpretación del espacio físico que le rodea para dar un adecuado y necesario uso, y, en ciertos casos, transformarlo, respetando la Naturaleza.
Elementos de Euclides
Los Elementos de Euclides se utilizaron como texto para la enseñanza de la Geometría durante 2.000 años, e incluso hoy, una versión modificada de sus primeros libros constituye la base de la enseñanza de la geometría plana en las escuelas primarias y secundarias en casi todos los países. La primera edición impresa de las obras de Euclides que apareció en Venecia en 1482, fue una traducción del árabe al latín, pues el texto original se considera hasta hoy desaparecido. Euclides parte de un conjunto suficientemente breve y sencillo de proposiciones iniciales – que no se demuestran – y desarrolla el discurso de una manera rigurosamente lógica, siguiendo las pautas que había trazado antes Platón (428 – 347 a.n.e.) para el desarrollo de una teoría por vía deductiva. Los restantes resultados se obtuvieron por deducción lógica en lugar de por generalización de resultados obtenidos de manera empírica. Se considera desde entonces que esta es la forma correcta de presentar cualquier teoría matemática.
Resumen de Geometría Plana
Ángulos
Definición : Unión o intersección de dos semiplanos cuyos bordes se cortan o intersecan.
Clasificación de ángulos según su amplitud
c) Obtuso: mayor que 90º y menor que 180º.
e) Sobreobtuso: mayor que 180º y menor que 360º.
Otros ángulos
a) Consecutivos: ángulos que tienen en común el vértice y un lado.
b) Adyacentes: ángulos consecutivos situados a un lado de una recta.
c)Opuestos por el vértice: ángulos que tienen el mismo vértice y sus lados están formados por semirrectas opuestas.
d)Correspondientes: situados a un mismo lado de la secante, uno es interno y otro externo.
e)Conjugados: situados a un mismo lado de la secante, ambos son internos o ambos son externos.
f)Alternos: situados a diferentes lados de la secante, ambos son internos o ambos son externos.
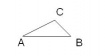
Triángulos
Definición : Polígono que tiene tres lados.
Clasificación
a)Según sus lados:
Equilátero: Sus tres lados tienen igual longitud. I
sósceles: Dos de sus lados tienen igual longitud.
Escaleno: Sus tres lados son diferentes.
b)Según sus ángulos:
Acutángulo: Sus tres ángulos son agudos.
Obtusángulo: Tiene un ángulo obtuso.
Rectángulo: Tiene un ángulo recto.
Propiedades de los triángulos
a)La suma de las amplitudes de los ángulos interiores es igual a 180º.
b)La amplitud de cada ángulo exterior es igual a la suma de las amplitudes de los dos ángulos interiores no adyacentes a él.
c)A ángulos iguales se oponen lados iguales y viceversa.
d)A mayor lado se opone el mayor ángulo y viceversa.
e)La suma de dos lados cualesquiera es siempre mayor que el tercer lado (desigualdad triangular).
Rectas notables en los triángulos
Mediatriz de un segmento: Recta perpendicular al segmento que pasa por su punto medio.
1. Los puntos de la mediatriz equidistan de los extremos del segmento.
Las mediatices de un triángulo: Rectas perpendiculares a cada lado y que cortan a estos en su punto medio. El punto de intersección de las mediatices de llama circuncentro (M) y está:
- Dentro del triángulo si este es acutángulo.
- Fuera del triángulo si este es obtusángulo.
- Sobre la hipotenusa si este es rectángulo.
Alturas del triángulo : Segmentos de perpendiculares trazadas desde los vértices de triángulo a las rectas que contienen a los lados opuestos. El punto de intersección de las alturas se llama ortocentro (H) y está:
- Dentro del triángulo si este es acutángulo.
- Fuera del triángulo si este es obtusángulo.
- Coincide con el vértice del ángulo recto si es rectángulo.
Medianas del triángulo: Segmentos determinados por los vértices del triángulo y el punto medio de sus lados opuestos. El punto de intersección de las medianas se llama baricentro (G) y siempre es un punto interior de este.
Bisectrices de un triángulo
Bisectriz de un ángulo: Semirrecta cuyo origen es el vértice del ángulo y lo divide en dos partes iguales.
- Todos los puntos de la bisectriz equidistan de los lados del ángulo.
Bisectrices de un triángulo: Segmentos de las bisectrices de los ángulos del triángulo determinados por los vértices de estos y el punto de intersección de los lados opuestos. El punto de intersección de las bisectrices del triángulo se llama incentro (I), es siempre interior al mismo y equidista de sus lados.
Generalidades
a)Triángulo equilátero: Como sus tres lados son iguales:
- Sus tres ángulos son iguales a 60º.
- Sus rectas notables coinciden.
b)Triángulo isósceles:
- Como tiene dos lados iguales, sus ángulos base también lo son.
- Las rectas notables respecto a la base coinciden.
c)Triángulo rectángulo:
- El lado que se opone al ángulo recto se le llama hipotenusa (mayor lado) y los otros dos catetos.
- Teorema de Pitágoras: En todo triángulo rectángulo el cuadrado de la longitud de la hipotenusa es igual a la suma del cuadrado de las longitudes de sus catetos.
- En todo triángulo rectángulo que tenga un ángulo de 30º, la longitud del lado opuesto a este es igual a la mitad de la hipotenusa.
Fórmulas
Cuadriláteros
Definición : Polígono que tiene cuatro lados.
Polígono: Región del plano limitada por un número finito de segmentos de rectas (lados del polígono) que se unen por su extremo (vértices).
Clasificación
Cuadriláteros :
Paralelogramos: sus dos pares de lados opuestos son paralelos
Trapecio: un par de lados opuestos paralelos.
Trapezoides: no tienen lados paralelos.
Paralelogramos
Rectángulo: Paralelogramo que tiene sus cuatro ángulos rectos.
Rombo: Paralelogramo que tiene sus cuatro lados iguales.
Cuadrado: Paralelogramo que tiene sus cuatros lados y sus cuatro ángulos iguales.
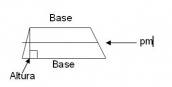
Trapecios
a) Las bases son los lados paralelos.
b) La altura es la distancia desde un vértice a la base opuesta.
c) La paralela media es el segmento que une los puntos medios de los lados no paralelos.
Clasificación.
Trapecio isósceles: Tiene dos lados no paralelos iguales.
- Los ángulos adyacentes a una misma base iguales.
- Sus diagonales son iguales.
Trapecio rectángulo: Tiene dos ángulos rectos.
Trapecio escaleno: Tiene sus lados no paralelos desiguales.
Propiedades
1. La suma de sus ángulos interiores es 360º(todos).
2. Los lados y ángulo opuestos son iguales (todos excepto el trapecio).
3. Las diagonales se intersecan en su punto medio (todos excepto trapecio).
4. Las diagonales son iguales (rectángulos y cuadrados).
5. Las diagonales son perpendiculares y bisectrices de los ángulos cuyos vértices se unen (rombo y cuadrado).
6. La paralela media es paralela a las bases y su longitud es igual a la semisuma de las longitudes de las bases (todos).
Área y Perímetro
Criterio de igualdad de triángulos
Dos triángulos son iguales si tienen:
Un lado y los ángulos adyacentes a él respectivamente iguales (teorema a.l.a.)
Dos lados y el ángulo comprendido entre ellas respectivamente iguales (teorema l.a.l )
Sus tres lados respectivamente iguales (teorema l.l.l.)
Dos triángulos rectángulos son iguales si tienen respectivamente iguales:
- La hipotenusa y un ángulo agudo
- La hipotenusa y un cateto
- Un cateto y un ángulo agudo
- Los dos catetos
Transversales
Teorema de las transversales:
Si dos semirrectas de origen común son cortadas por rectas paralelas entonces:
1ra parte: La razón entre dos segmentos de una misma semirrecta es igual a la razón entre los dos segmentos correspondientes en otra semirrecta.
2da parte: La razón entre dos segmentos de una semirrecta es igual a la razón entre los dos segmentos de paralelas correspondientes (uno de los extremos de los segmentos de semirrectas coinciden con el vértice)
3ra parte: La razón entre dos segmentos de paralelas es igual a la razón entre los dos segmentos de paralelas correspondientes.
Circunferencia y Círculo
Definiciones :
a)Circunferencia: Conjunto de todos los puntos de plano situados a la misma distancia de un punto fijo de dicho plano.
b)Círculo: Área o superficie plana formada por todos los puntos de una circunferencia y sus puntos interiores.
Elementos: Radio, diámetro, cuerda, arco, centro.
d =2r
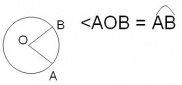
c)Ángulo central: Ángulo que tiene su vértice en el centro de la circunferencia.
d)Ángulo inscrito: Ángulo cuyo vértice pertenece a la circunferencia y sus lados la intersecan.
Teoremas y relaciones
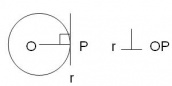
1- La recta tangente a una circunferencia es perpendicular al radio que tiene como extremo al punto de tangencia.
2- La amplitud del ángulo central es igual a la de su arco correspondiente.
3- La amplitud de todo ángulo inscrito es igual a la mitad de su arco correspondiente (y de su ángulo central correspondiente).
4- En una misma circunferencia o en circunferencias iguales, a ángulos centrales iguales corresponden arcos (y cuerdas) iguales.
5- En una misma circunferencia o en circunferencias iguales, a mayor cuerda corresponde mayor arco (y viceversa).
6- Los ángulos inscritos que le corresponde el mismo arco son iguales.
7- Todo radio perpendicular a una cuerda la divide en dos partes iguales.
8- Todo ángulo inscrito cuyo arco correspondiente es una semicircunferencia es un ángulo recto (teorema de Tales).
9- Todo triángulo rectángulo se puede inscribir en una circunferencia cuyo centro es el punto medio de la hipotenusa.
Área y Longitud
Fuentes
- Libros de textos de Matemática de 6to, 7mo, 8vo y 9no Grado.
- Cuadernos de trabajo de Matemática de 7mo, 8vo y 9no Grado.
- Revista Cultural de Cumanayagua
- Eves, Howard. Estudio de las geometrías. Editorial UTEHA. 1969.
- Hogben, Lancelot. La Matemática al alcance de todos. Buenos Aires., s.a
- Ríbnikov, H. Historia de las Matemáticas. Editorial Mir. Moscú. 1987.
- Wussing, H. Conferencias sobre historia de la Matemática. La Habana : Editorial Pueblo y Educación,1989.