Johannes Kepler
| ||||||||||||||||
Johannes Kepler. Astrónomo y filósofo alemán, famoso por formular y verificar las tres leyes del movimiento planetario conocidas como leyes de Kepler. Fue colaborador de Tycho Brahe, a quien sustituyó como matemático imperial de Rodolfo II. En 1935 la UAI decidió en honor llamarle «Kepler» a un astroblema lunar.
Sumario
Síntesis biográfica
Infancia
Nació en 1571 en el ducado alemán de Wurttemberg. De niño padeció diversas enfermedades tales como miopía, dolores de cabeza, afecciones estomacales. A la edad de tres años, contrae la viruela, lo que, entre otras secuelas, debilitará la vista severamente. A pesar de la salud, fue un niño brillante que gustaba impresionar a los viajeros en el hospedaje de su madre con sus fenomenales facultades matemáticas. En 1584 ingresó al seminario protestante de Adelberg.
Estudios
A partir de 1589 estudió Teología en la Universidad de Tübingen. Allí tuvo como Profesor de Matemáticas a Maestlin, que conocía y compartía la Teoría Heliocéntrica de Copérnico. Él, que era un pitagórico y veía en Dios al supremo geómetra creador de un universo armónico, vio en la simplicidad de esta teoría un rasgo del plan creador de Dios.
Continúa allí con los estudios después de obtener una maestría en 1591.
Matrimonio
Estuvo casado dos veces. El primer matrimonio, de conveniencia, el 27 de abril de 1597 con Barbara Müller. Este matrimonio, organizado por los allegados, lo unió a una mujer "grasa y simple de espíritu", con carácter execrable.
Trayectoria académica
En 1594 marchó de Tübingen a Graz, en Austria, donde ejerció la docencia en la universidad como profesor de Aritmética, Geometría y Retórica, dedicando tiempos libres a la Astronomía. En la época, la distinción entre ciencia y creencia no estaba establecida todavía claramente y el movimiento de los astros, todavía bastante desconocido, se consideraba gobernado por leyes divinas. En Graz, publica almanaques con predicciones astrológicas - que los realizaba - aunque él negaba algunos de los preceptos. En la época, la distinción entre ciencia y creencia no estaba establecida todavía claramente y el movimiento de los astros, todavía bastante desconocido, se consideraba gobernado por leyes divinas.
En 1600 Pasó entonces a Praga (hoy capital de la República Checa), invitado por el famoso astrónomo Tycho Brahe, quien se puso en contacto con él, luego de leer el libro. El maestro murió al año siguiente y Kepler lo reemplazó como matemático y astrónomo de la corte del emperador.
Mantenía un sistema combinado, heliocéntrico y geocéntrico. Kepler redujo sus descripciones geocéntricas al heliocentrismo. A pesar de ello, seguía encontrando graves desacoples entre el desplazamiento que, según los cálculos, los cuerpos celestes debían realizar y el que efectivamente realizaban. Esta situación lo llevó a pensar que, siendo el Sol el agente que ejerce la fuerza que hace girar a los planetas a su alrededor, al aumentar la distancia entre un planeta y el Sol, la velocidad del desplazamiento debía disminuir. Para afirmar esto tuvo que rechazar la milenaria concepción de las órbitas circulares.
En 1612 fue nombrado matemático de los estados de la Alta Austria (distrito de Linz). A pesar de los descubrimientos, Kepler no estaba satisfecho. Convencido de que la armonía y la simplicidad gobiernan el Universo, pretendía encontrar una relación simple entre los tiempos de revolución de los planetas (períodos orbitales) y la distancia al Sol.
Más de nueve años le tomó encontrar esta relación y formular la tercera ley del movimiento de los planetas: el período es proporcional al semieje mayor de la elipse elevado a 3/2.
En 1628 pasó al servicio de A. von Wallenstein, en Sagan (Silesia), quien le prometió, en vano, resarcirle de la deuda contraída con él por la Corona a lo largo de los años. Un mes antes de morir, víctima de la fiebre, Kepler había abandonado Silesia en busca de un nuevo empleo.
Muerte
Murió en 1630 en Ratisbona, mientras viajaba con la familia de Linz a Sagan. En la lápida fue grabado el siguiente epitafio, compuesto por él mismo: Medí los cielos, y ahora las sombras mido. En el cielo brilló el espíritu. En la tierra descansa el cuerpo.
Obra científica
En 1594, cuando Kepler dejó Tübingen y marchó a Graz (Austria), elaboró una hipótesis geométrica compleja para explicar las distancias entre las órbitas planetarias - órbitas que se consideraban circulares erróneamente.
(Posteriormente, Kepler dedujo que las órbitas de los planetas son elípticas; sin embargo, estos primeros cálculos sólo coinciden en un 5% con la realidad.) Planteó que el Sol ejerce una fuerza que disminuye de forma inversamente proporcional a la distancia e impulsa a los planetas alrededor de sus órbitas.
Publicó las teorías en un tratado titulado Mysterium Cosmographicum en 1596. Esta obra es importante porque presentaba la primera demostración amplia y convincente de las ventajas geométricas de la teoría copernicana.En 1597 año publicó Mysterium Cosmographicum, dejando constancia de las ventajas que desde el punto de vista geométrico ofrecía la Teoría Heliocéntrica.
Por ese entonces aún consideraba que las órbitas planetarias eran circulares. Kepler fue profesor de astronomía y matemáticas en la Universidad de Graz desde 1594 hasta 1600, cuando se convirtió en ayudante del astrónomo danés Tycho Brahe en el observatorio de Praga. A la muerte de Brahe en 1601, Kepler asumió su cargo como matemático imperial y astrónomo de la corte del emperador Rodolfo II.
Una de sus obras más importantes durante este periodo fue Astronomía nova (1609), la gran culminación de sus cuidadosos esfuerzos para calcular la órbita de Marte, dedicada a exponer sus cálculos sobre la órbita de este planeta. En ella expone dos de sus tres famosas "leyes del movimiento de los planetas", hoy llamadas "leyes de Kepler". En 1610 publicó Dissertatio cum Nuncio Sidereo, sobre las observaciones de Galileo y, al año siguiente, realizó sus propias observaciones de los satélites descriptos por el italiano con la ayuda de un telescopio, publicando los resultados de dichas observaciones en su obra Narratio de Observatis Quatuor Jovis Satellitibus.
En 1612 se hizo matemático de los estados de la Alta Austria. Mientras vivía en Linz, publicó su Harmonices mundi, Libri (1619), obra en la que hizo pública su tercera ley: la relación lineal entre el cubo de la distancia promedio de un planeta al Sol y el cuadrado de su período de revolución.
Hacia la misma época publicó un libro, Epitome astronomiae copernicanae (1618-1621), que reúne todos los descubrimientos de Kepler en un solo tomo.
Igualmente importante fue el primer libro de texto de astronomía basado en los principios copernicanos, y durante las tres décadas siguientes tuvo una influencia capital convirtiendo a muchos astrónomos al copernicanismo kepleriano. La última obra importante aparecida en vida de Kepler fueron las Tablas rudolfinas (1625). Basándose en los datos de Brahe, las nuevas tablas del movimiento planetario reducen los errores medios de la posición real de un planeta de 5 °a 10'.
El matemático y físico inglés sir Isaac Newton se basó en las teorías y observaciones de Kepler para formular su ley de la gravitación universal. Kepler se destacó también por sus aportes a la óptica, formuló:
- Ley Fundamental de la Fotometría
- Reflexión total
- Formuló la primera Teoría de la Visión moderna
- Desarrolló un Sistema Infinitesimal, antecesor del Cálculo Infinitesimal de Leibnitz y Newton.
Las tres leyes de Kepler
El astrónomo alemán (1571-1630) formuló las tres famosas leyes que llevan su nombre después de analizar un gran número de observaciones realizadas por Tycho Brahe (1546-1601) de los movimientos de los planetas, sobre todo de Marte. Kepler, haciendo cálculos sumamente largos, encontró que había discrepancias entre la trayectoria calculada para Marte y las observaciones de Tycho, diferencias que alcanzaban en ocasiones los 8 minutos de arco (las observaciones de Tycho poseían una exactitud de alrededor de 2 minutos de arco) Estas diferencias lo llevaron a descubrir cual era la verdadera órbita de Marte y los demás planetas del Sistema Solar.
1ra Ley. Orbitas elípticas
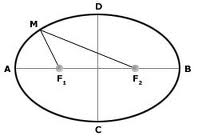
Las órbitas de los planetas son elipses que presentan una pequeña excentricidad y en donde el Sol se localiza en uno de sus focos. Una elipse es básicamente un círculo ligeramente aplastado. Técnicamente se denomina elipse a una curva plana y cerrada en donde la suma de la distancia a los focos (puntos fijos, F1 y F2) desde uno cualquiera de los puntos M que la forman es constante e igual a la longitud del eje mayor de la elipse (segmento AB). El eje menor de la elipse es el segmento CD, es perpendicular al segmento AB y corta a este por el medio.
2da. Ley de las órbitas
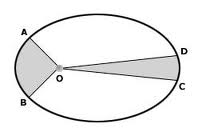
Las áreas barridas por el radio vector que une a los planetas al centro del Sol son iguales a tiempos iguales. La velocidad orbital de un planeta (velocidad a la que se desplaza por su órbita) es variable, de forma inversa a la distancia al Sol: a mayor distancia la velocidad orbital será menor, a distancias menores la velocidad orbital será mayor. La velocidad es máxima en el punto más cercano al Sol (perihelio) y mínima en su punto más lejano (afelio). El radio vector de un planeta es la línea que une los centros del planeta y el Sol en un instante dado. El área que describen en cierto intervalo de tiempo formado entre un primer radio vector y un segundo radio vector mientras el planeta se desplaza por su órbita es igual al área formada por otro par de radio vectores en igual intervalo de tiempo orbital.
En el gráfico superior: el tiempo que le toma al planeta recorrer del punto A al punto B de su órbita es igual al tiempo que le toma para ir del punto C al D, por tanto, las áreas marcadas OAB y OCD son iguales. Para que esto suceda, el planeta debe desplazarse más rápidamente en las cercanías del Sol (en el foco de la elipse, punto O del gráfico)
3ra.. Ley armónica
El 17 de octubre de 1604 observó una supernova en nuestra propia Galaxia, la Vía Láctea a la que más tarde se le llamaría la estrella de Kepler. La estrella había sido observada por otros astrónomos europeos el día 9 del mismo mes como Brunowski en Praga (quién escribió a Kepler), Altobelli en Verona y Clavius en Roma y Capra y Marius en Padua. Kepler inspirado por el trabajo de Tycho Brahe realizó un estudio detallado de su aparición. Su obra De Stella nova in pede Serpentarii ('La nueva estrella en el pie de Ophiuchus') proporcionaba evidencias de que el Universo no era estático y sí sometido a importantes cambios. La estrella pudo ser observada a simple vista durante 18 meses después de su aparición. La supernova se encuentra a tan solo 13000 años luz de nosotros. Ninguna supernova posterior ha sido observada en tiempos históricos dentro de nuestra propia galaxia. Dada la evolución del brillo de la estrella hoy en día se sospecha que se trata de una supernova de tipo I.
La estrella de Kepler
El 17 de octubre de 1604 observó una supernova en nuestra propia Galaxia, la Vía Láctea a la que más tarde se le llamaría la estrella de Kepler. La estrella había sido observada por otros astrónomos europeos el día 9 del mismo mes como Brunowski en Praga (quién escribió a Kepler), Altobelli en Verona y Clavius en Roma y Capra y Marius en Padua. Kepler inspirado por el trabajo de Tycho Brahe realizó un estudio detallado de la aparición. La obra De Stella nova in pede Serpentarii ('La nueva estrella en el pie de Ophiuchus') proporcionaba evidencias de que el Universo no era estático y sí sometido a importantes cambios.
La estrella pudo ser observada a simple vista durante 18 meses después de la aparición. La supernova se encuentra a tan solo 13000 años luz de nosotros. Ninguna supernova posterior ha sido observada en tiempos históricos dentro de nuestra propia galaxia. Dada la evolución del brillo de la estrella hoy en día se sospecha que se trata de una supernova de tipo I.
Obras de Kepler
A lo largo de la vida, publicó las siguientes obras, ordenadas cronológicamente:
- Mysterium cosmographicum (El misterio cósmico, 1596).
- Astronomiae Pars Optica (La parte óptica de la astronomía, 1604).
- De Stella nova in pede Serpentarii (La nueva estrella en el pie de Ophiuchus, 1604). El 17 de Octubre de 1604 Kepler observó la aparición de una nueva estrella. El fenómeno, corroborado por otros astrónomos europeos, le interesó profundamente. Aparte del interés astronómico, se trataba de una cuestión filosófica esencial, ya que Kepler defendió siempre que el universo no era algo estático. Actualmente se sabe que se trataba de una supernova de clase I. Astronomia nova (Nueva astronomía, 1609).
- Dioptrica (Dioptrio, 1611). Debido a la miopía que padecía, Kepler se interesó siempre por la óptica. Los resultados prácticos de esta obra se tradujeron en gafas que ayudaban a ver mejor a los miopes y présbitas y también en el diseño de un nuevo telescopio que se utilizó en astronomía durante años, el telescopio Kepler.
- De Vero Anno quo Aeternus Dei Filius Humanam Naturam in Utero Benedictae Virginis Mariae Assumpsit (1613). Se trata de un curioso y breve escrito en el que Kepler demostraba que Jesús había nacido en el año 4 a.C.
- Epitome astronomiae Copernicanae (publicado en tres partes, 1618-1621).* Harmonice Mundi (La armonía de los mundos, 1619).* Tabulae Rudolphinae (1627).
- Somnium (El sueño, 1634), relato fantástico en el que los protagonistas contemplan extasiados el espectáculo de la Tierra girando sobre sí misma. Y es que a Kepler se le puede considerar como el primer autor de ciencia ficción de la historia.*Aparte de su vida como astrónomo y matemático, Kepler llegó a ser un astrólogo de renombre. Dos pronósticos importantes, uno sobre cosechas y otro sobre el desenlace de una batalla contra los turcos, le acreditaron como un maestro en el arte de descifrar los oráculos de las estrellas. Esta actividad, de la que Kepler no se sentía especialmente orgulloso, le supuso un importante respaldo económico en momentos difíciles. En una ocasión Kepler manifestó: “La ramera Astrología debe sustentar a su madre, la Astronomía, ya que los salarios de los matemáticos son tan exiguos que inevitablemente la madre debería pasar hambre si la hija nada ganase”, declaración que no deja dudas sobre la opinión que la Astrología le merecía.
- Las Tablas Rudolfinas . Las Tablas Rudolfinas no son tan conocidas como sus famosas leyes del movimiento planetario y sin embargo constituyen una de las obras cumbres de Kepler, una pieza clave en el nacimiento de la nueva astronomía. Esta tablas fueron un encargo que el Rey Rodolfo II (de ahí el nombre de las tablas) hizo a Tycho Brahe y que, posteriormente, fue encomendado a Kepler, que aplicó las nuevas teorías para perfeccionar los cálculos de las posiciones del Sol y la Luna, con sus correspondientes eclipses, para cualquier fecha anterior o posterior a la era cristiana. Se trata de un trabajo realmente titánico del que dan testimonio los cientos de páginas con miles de cálculos que Kepler tuvo que realizar a los largo de 22 años. Por suerte, una gran parte de los cálculos se vieron favorecidos por la aparición de los logaritmos de Napier, cuya práctica perfeccionó Kepler. Las Tablas Rudolfinas resultaron ser imprescindibles para la confección de calendarios de efemérides y para la navegación durante más de 200 años.