Ligadura (Mecánica teórica)

Enlace o ligadura Concepto: Todo lo que restringe los desplazamientos de un cuerpo en el espacio.

Enlace o ligadura. En Mecánica teórica, es todo lo que restringue los desplazamientos de un cuerpo en el espacio.

Grado de libertad de un cuerpo

El número de coordenadas independientes que determinan la posición de cualquier cuerpo o sistema material se denomina grado de libertad de un cuerpo.

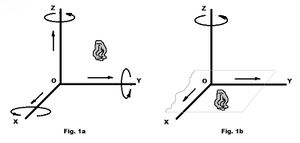
El concepto grado de libertad, se puede analizar, si se toma un cuerpo cualquiera que se encuentre en el espacio y se toma como referencia un sistema coordenado rectangular.

Este cuerpo posee seis grados de libertad, o sea, que los movimientos rectilíneos respecto a los ejes coordenadas X, Y, Z, constituyen tres grados de libertad, y los movimientos de rotación respecto a estos ejes, también constituyen tres grados de libertad.

Este mismo cuerpo si se coloca sobre el plano X o Y. Sólo quedarán tres grados de libertad: dos desplazamientos y un movimiento de rotación respecto al eje Z.

Grado de libertad

Cualquier cuerpo rígido puede hallarse en el espacio en estado libre o dependiente (ligado). Si un cuerpo rígido es capaz de desplazarse en cualquier dirección, este cuerpo se denomina libre. Si un cuerpo rígido topa con algún obstáculo en su camino, impidiéndole su movimiento, este cuerpo se denomina dependiente (ligado). De aquí se deduce, que todo lo que restringe los desplazamientos de un cuerpo en el espacio se denomina ligadura. En el ejemplo estará ligado al plano X o Y.

En la solución de la mayoría de los problemas de la Mecánica hay que tratar con cuerpos no libres, o sea, con cuerpos que tienen contacto o están sujetos a otros cuerpos, en virtud de lo cual se hacen imposibles unas u otras translaciones del cuerpo. Si el cuerpo ejerce presión sobre el enlace, bajo la acción de las fuerzas aplicadas, el enlace a su vez actuará sobre el cuerpo dado, es decir, que la fuerza con la cual un enlace actúa sobre el cuerpo, obstaculizando su traslación en una u otra dirección se denomina fuerza de reacción o simplemente reacción de este enlace. .

Según la ley de igualdad de la acción y reacción, (tercera ley de Newton), la fuerza de reacción de un enlace es igual en módulo a la fuerza de presión sobre el enlace y está orientada en sentido contrario a esta fuerza, es decir, en sentido opuesto al sentido en el cual el enlace obstaculiza la traslación del cuerpo. La mayoría de los problemas técnicos de la Estática consiste precisamente en la determinación de las fuerzas de reacción de los enlaces. Conociendo estas fuerzas se puede conocer también las fuerzas de presión sobre los enlaces, o sea, se obtendrán los datos necesarios para calcular la resistencia de las construcciones

Tipos de enlaces

Algunos tipos de ligaduras suponiéndolas hechas de materiales rígidos sin rozamiento en los puntos de contacto con los cuerpos examinados.

Contacto entre cuerpos

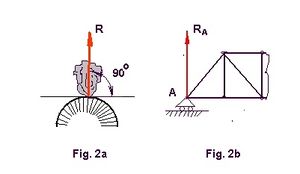
1. El cuerpo se apoya en el punto A de una superficie lisa. La superficie se llama lisa si se puede prescindir del rozamiento de un cuerpo contra ella. Puesto que la superficie de apoyo lisa no obstaculiza el resbalamiento de la superficie de un cuerpo sobre ella, la reacción R de la superficie lisa siempre está orientada según la normal común a la superficie del cuerpo y a la superficie del enlace en el punto de contacto de las mismas.
2. A este tipo de ligaduras se puede referir el llamado rodillo móvil. Aquí la viga o armadura, con ayuda de un balancín, tiene apoyado su extremo A sobre un rodillo cilíndrico. La reacción RA está aplicada a la viga en el punto A y dirigida normalmente a la superficie de apoyo, sobre la cual los rodillos pueden rodar.

Rodillo móvil

Enlace flexible

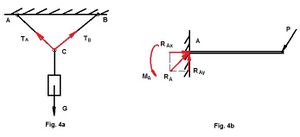
En este caso, las ligaduras o enlaces son los hilos que retienen el cuerpo. Si en calidad de ligaduras se utilizan cuerpos flexibles (hilo, cable, cadena) las fuerzas de reacción TA y TB se aplican al cuerpo en los puntos de sujeción y se dirigen a lo largo de los hilos.

Empotramiento rígido

La viga AB tiene uno de sus extremos rígidamente empotrado en un muro, el otro extremo de ésta sirve de apoyo para una construcción. En el empotramiento se originan unas reacciones compuestas por una fuerza que es la reacción del empotramiento RA y su par, el momento de empotramiento MA.

Diagramas de fuerzas

El equilibrio de los cuerpos ligados, se estudia en la Estática con fundamento en el axioma siguiente: "todo cuerpo ligado puede considerarse como libre si suprimimos las ligaduras y sustituimos sus acciones por las reacciones de estas ligaduras (incluyendo su propio peso)", (esto se denomina diagrama de fuerzas o cuerpo libre). .

Empotramiento

Al resolver un problema en el que interviene el equilibrio de un sólido rígido, es esencial el considerar todas las fuerzas que actúen sobre el mismo; es igualmente importante el excluir cualquier fuerza que no esté directamente aplicada al sólido. El omitir una fuerza o añadir otra extraña destruye las condiciones de equilibrio. Por tanto, el primer paso para la solución del problema debe consistir en dibujar un diagrama libre del sólido rígido en estudio. Por su importancia resumiremos los pasos que se deben seguir al dibujar un diagrama de cuerpo libre.

1. Tomar una decisión clara respecto a la elección del sólido libre a emplear. Este cuerpo se separa entonces de su base de sustentación, así como de cualquier otro cuerpo. A continuación se realiza un croquis del contorno del cuerpo aislado.
2. Se indican todas las fuerzas externas que representan la acción ejercida sobre el cuerpo rígido por la base de sustentación y por los cuerpos que le han sido separados; estas fuerzas deben aplicarse en los diversos puntos por los que estaban soportado el cuerpo libre en su base de sustentación o por los que estaba conectado a los otros cuerpos. Se debe incluir también entre las fuerzas externas el peso del sólido libre, ya que representa la atracción ejercida por la tierra sobre las diversas partículas que componen el cuerpo libre. Debe aplicarse en el centro de gravedad del cuerpo.
3. El módulo, la dirección y el sentido de las fuerzas externas conocidas debe marcarse claramente en el diagrama. Hay que tener cuidado en indicar el sentido de la fuerza ejercida sobre el cuerpo libre. Las fuerzas externas conocidas comprenden generalmente el peso del cuerpo libre y las fuerzas aplicadas con un propósito determinado.
4. El diagrama del cuerpo libre debe incluir también dimensiones, ya que pueden necesitarse para el cálculo de momentos de las fuerzas.

Ejemplo de diagrama de fuerzas

Diagrama de fuerzas

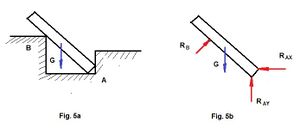
La barra lisa que se apoya en el punto A sobre el piso y la pared y en B sobre un poste (Fig. 5a). Cuando una de las superficies en contacto es un punto, la reacción está dirigida por la normal a la otra superficie. Puede considerarse como un cuerpo libre (Fig. 5b) que se encuentra en equilibrio bajo la acción de la fuerza conocida G (peso de la viga) y las reacciones de las ligaduras: RAX, RAY y RB.

Fuentes

1. Ballester Gouraige, Andrés. Fundamentos de Mecánica Teórica y Teoría de los Mecanismos. Editado Departamento E.T.P... I.S.P. "Raúl Gómez García", Guantánamo. 1995.
2. Nikitin, E.M. Mecánica Teórica para las escuelas de peritaje. Ed. MIR, Moscú, 1980.
3. Sokolov, F y P. Usov. Mecánica Industrial. Tercera edición. Ed. MIR, Moscú, 1986.
4. Starzhinski, V.M. Mecánica Teórica. Ed. MIR, Moscú, 1980.
5. Targ, S.M. Curso breve de Mecánica Teórica. Cuarta edición. Ed. MIR, Moscú, 1976.