Magnitud estelar
| ||||
Magnitud estelar aparente. Es la medida utilizada para medir el brillo aparente de las estrellas, del Sol, de la Luna, los planetas u otros cuerpos celestes. Utilizando una ecuación matemática podemos determinar la cantidad de luz que se recibe del objeto sin que interfiera la atmósfera terrestre u cualquier otro factor.
Concepto
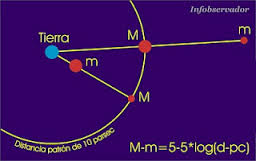
Se denomina magnitud estelar aparente debido a que no depende de la distancia a que se encuentre. Un objeto puede ser más brillante que otro, pero si está más lejos puede tener una brillo aparentemente menor. Se puede utilizar el término de magnitud absoluta al brillo de los objetos suponiendo que se encuentran a una distancia fija de 10 parsecs.
Orígenes
Esta escala tiene sus orígenes en la práctica de la Grecia antigua de clasificar las estrellas en 6 magnitudes, desde la primera hasta la sexta magnitud. A las estrellas más brillantes se les clasificaba como de primera magnitud (m=+1) y a medida que a simple vista disminuían su brillo se clasificaban de segunda, tercera, cuarta, quinta y finalmente, de clasificaban de sexta magnitud (m=+6) aquellas estrellas apenas perceptibles por el ojo humano en condiciones muy favorables de observación, sin ayuda de ningún telescopio.
Este método primitivo para indicar el brillo de estrellas fue popularizado por el sabio griego Ptolomeo en su obra “Almagesto”, aunque su invención se le atribuye al astrónomo Hiparco de Nicea. Este sistema original no medía la magnitud del Sol. Debido al hecho de que la respuesta del ojo humano a la luz es logarítmica la escala que resulta es también logarítmica.
Se establece que cada magnitud aparente es 2.512 veces menos brillante que la anterior, de esta manera las estrellas de segunda magnitud son 2.512 veces menos brillantes que las de primera, las de tercera magnitud son 2.512 veces menos brillantes que las de segunda y así sucesivamente hasta llegar a las de sexta magnitud, que entonces serían 100 veces menos brillantes que las de primera magnitud. A este número irracional (2.512) se le conoce como cociente de Pogson.
Sistema actual
El sistema moderno no está limitado a 6 magnitudes y los objetos más brillantes pueden tener magnitudes negativas. Por ejemplo Sirio, la estrella más brillante, tiene una magnitud aparente de -1,47. La escala moderna incluye a la Luna y al Sol; la Luna en su fase de luna llena tiene una magnitud aparente de -12,6 y el Sol tiene una magnitud aparente de -26,7. Los telescopios Hubble y Keck han localizado estrellas con magnitudes de +30. La magnitud aparente se puede definir como: Archivo:Formula magnitud estelar.JPG donde Fx es el flujo observado en la banda x, y C es una constante que depende de las unidades de flujo y de la banda. De esta manera se calculan las magnitudes estelares que permiten clasificar por su brillo a los cuerpos celestes.
| Magnitud aparente |
Objeto celeste |
|---|---|
| −26.7 | El Sol |
| −12.6 | Luna llena |
| −4.4 | Máximo brillo del planeta Venus |
| −2.8 | Máximo brillo del planeta Marte |
| −1.5 | Estrella más brillante: Sirio |
| −0.76 | Segunda estrella más brillante: Canopo |
| +3.0 |
Estrellas más débiles visible desde las ciudades |
| +6.0 |
Estrellas más débiles visibles al ojo humano |
| +12.6 |
Quásar más brillante |
| +30.0 |
Objetos más débiles detectados con el telescopio |
Es importante destacar que la magnitud aparente de algunos objetos estelares oscila periódicamente entre determinados valores. Es muy común este fenómeno en muchas estrellas, sobre todo en las que son en realidad sistemas de dos o más estrellas que rotan superponiéndose cada cierto intervalo de tiempo, pues cuando se eclipsan mutuamente el brillo disminuye.