Tangente
| ||||||
Tangente. Relativa a un ángulo agudo de un triángulo rectángulo, razón entre las longitudes del cateto opuesto y el cateto adyacente al ángulo.
Sumario
Razones en el triángulo rectángulo
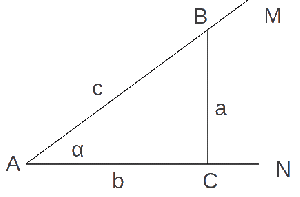
Las razones (cocientes) entre las longitudes de los lados de un triángulo rectángulo dependen solo de las amplitudes de sus ángulos agudos. Veamos esta afirmación con más detenimiento (figura 1):
Sea MAN un ángulo agudo.
Desde un punto cualquiera de uno de sus lados (B) distinto del vértice A consideremos una recta perpendicular al otro lado, formando el triángulo ABC rectángulo en C, o sea con catetos de longitudes a y b, e hipotenusa c.
Sea B' otro punto cualquiera (B' ≠ A) del lado AM y B un punto cualquiera (B ≠ A) del lado AN. Consideremos las perpendiculares B'C' y BC a AN y AM respectivamente. Los tres triángulos ABC, AB'C' y ABC tienen sus ángulos iguales (ya que son rectángulos y tienen un ángulo común), luego son semejantes, y como tales sus lados homólogos son proporcionales.
Tangente
Estas razones entre las longitudes de los lados de un triángulo rectángulo son de importancia fundamental en el estudio de la trigonometría. Para un ángulo agudo del triángulo rectángulo, a la razón entre la longitud del cateto opuesto al ángulo y la longitud del cateto adyacente al ángulo se le llama Tangente del ángulo y se denota por tan (tg), o sea:
tan α = a/b, y tan β = b/a
Por ser α y β ángulos complementarios, en las relaciones anteriores se observa que:
tan α = 1/(tan(90° - α))
Valores de la tangente para los ángulos notables de 30°, 45° y 60°
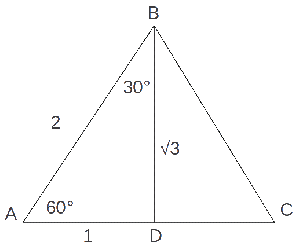
Consideremos un triángulo ABC equilátero de lado 2 (figura 2). Sea BD la perpendicular por B a AC. En en triángulo ADB rectángulo en D se tiene que el ángulo DAB mide 60° y el ángulo ABD mide 30°, AB = 2, AD = 1, BD = √3, por lo tanto:
tan 60° = √3
tan 30° = √3/3
Para comprobar que tan 45° = 1 basta considerar un triángulo rectángulo isósceles.