Triángulo
| ||||||
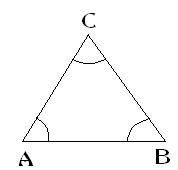
Triángulo(figura). Polígono de tres lados. La suma de los tres ángulos de un triángulo es 180º. Dos de los ángulos son, necesariamente, agudos. El tercero puede ser también agudo, o bien recto u obtuso.
Sumario
Definición
Un triángulo es un [polígono] de 3 lados, siendo el menor de los polígonos en cuanto a la cantidad de lados. Las longitudes de todos los lados deben satisfacer el teorema que dice " en todo triángulo la suma de dos lados es mayor que el tercer lado" [1].
Definición alternativa
Un triángulo es una figura de tres puntos que no están en una misma recta y de tres segmentos que unen dichos puntos de dos en dos. [2]
Como se sabe, tres puntos que no están en una misma recta determinan un plano y sólo uno; el triángulo, que definen tales puntos, está en un único plano; luego es una figura plana.
Regiones
Es un polígono convexo; no tiene diagonales; si se considera al triángulo como la unión de tres segmentos determinados por 3 puntos no colineales, el plano queda dividido en dos regiones disjuntas: interior y exterior; si se une un punto del interior con otro del exterior, el segmento que originan corta el triángulo; además cualquier segmento definido por dos puntos del interior no corta el triángulo; en el caso de un segmento que une dos puntos del exterior, dicho segmento no corta el triángulo. Por un punto del exterior se puede trazar al menos una recta que no corta al triángulo. Cualquier recta que pasa por un punto del interior, siempre corta el triángulo, el interior no puede contener una recta. [3]
A la unión del interior con los lados AB, BC y AC, se denomina región triangular; como tal tiene área.
Clasificación
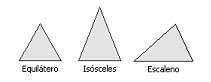
Los triángulos se clasifican según la longitud de sus lados o según la amplitud de sus ángulos.
Según sus lados
Según la longitud de sus lados, los triángulos se clasifican en:
- Triángulo equilátero: si sus tres lados son iguales.
- Triángulo isósceles: si tienen dos lados iguales.
- Triángulo escaleno: si los tres lados son distintos.
Según sus ángulos
La clasificación según sus ángulos los define en las siguentes categorías:
- Triángulo acutángulo: Si todos los ángulos del triángulo son agudos.
- Triángulo rectángulo: Si tiene un ángulo recto. Estos triángulos también se denominan rectos.
- Triángulo obtusángulo: Estos triángulos poseen un ángulo obtuso.
- Un triángulo que no es rectángulo se llama triángulo oblicuángulo [4]
Elementos diversos
Alturas de un triángulo
Se llama base de un triángulo a cualquiera de sus lados. El segmento perpendicular desde un vértice a la base opuesta o a su prolongación se llama altura. Un triángulo tiene, pues, tres bases a, b, c, y las tres alturas correspondientes, ha, hb y hc.
En un triángulo rectángulo el cuadrado de la altura sobre la hipotenusa es igual al producto de los dos segmentos en que la divide: h2 = m • n
Las tres rectas que contienen respectivamente a las tres alturas de un triángulo se cortan en un punto llamado ortocentro. Si el triángulo es acutángulo, el ortocentro es un punto interior del triángulo.
En un triángulo rectángulo, cada cateto puede ser considerado como base y como altura. El ortocentro es, por tanto, el vértice del ángulo recto. Si el triángulo es obtusángulo el ortocentro se obtiene, prolongando las alturas, en el exterior del triángulo.
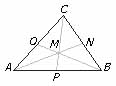
Medianas
Se llama mediana de un triángulo a cada uno de los tres segmentos que unen un vértice con el punto medio del lado opuesto. Las tres medianas de un triángulo se cortan en un punto que se llama baricentro.
El baricentro corta a cada mediana en dos segmentos, uno de ellos la mitad del otro:
Mediatrices
La mediatriz de un triángulo es la recta mediatriz de cualquiera de sus lados. Es la recta perpendicular que pasa por el punto medio de cualquiera de los tres lados. Hay tres mediatrices que concurren en un punto llamado circuncentro, que viene a ser ser el centro de la circunferencia circunscrita al triángulo del caso. [5]
Bisectrices
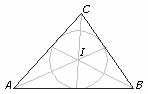
La bisectriz de un triángulo es un segmento que une un vértice con un punto del lado opuesto y es parte de la bisectriz del ángulo formado por los lados que concurren en tal vértice.Las tres bisectrices convergen en un único punto, llamado incentro, que también es el centro de la circunferencia inscrita al triángulo en cuestión. [6]
Cevianas
una ceviana es un segmento que une un vértice cualquiera del triángulo con su respectivo lado opuesto. Hay una infinidad de cevianas que parten de un vértice. Sus comportamientos los expresa el teorema de Ceva.
Circunferencia inscrita
Las bisectrices de los tres ángulos de un triángulo se cortan en un punto que se llama incentro porque es el centro de la circunferencia inscrita que es tangente a los tres lados del triángulo. Ésta es la mayor circunferencia contenida en el triángulo.
Circunferencia exinscritas
La bisectriz interior de un ángulo se corta con las dos bisectrices exteriores de los otros dos ángulos en un punto llamado exincentro, y que es centro de una circunferencia (exinscrita) tangente a un lado y a la prolongación de los otros dos.
Un triángulo tiene, pues, tres circunferencias exinscritas.
Circunferencia circunscrita
Las mediatrices de los lados de un triángulo se cortan en un punto llamado circuncentro porque es centro de la circunferencia circunscrita que pasa por los tres vértices del triángulo. Esta es la menor circunferencia que contiene al triángulo.
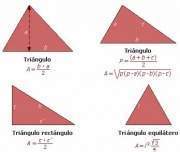
Área de un Triángulo
El Área de un triángulo de lados a, b, c, y alturas correspondientes ha, hb y hc es: A = (1/2)a • ha = (1/2)b • hb = (1/2)c • hc
Si se conocen las longitudes de los tres lados, a, b, c, el área se puede calcular mediante la siguiente fórmula, llamada fórmula de Herón:
en donde p = (a + b + c)/2 es el semiperímetro del triángulo.
Topología del triángulo
Se va a usar la topología común o euclídea del plano.
- Un punto es punto interior de un triángulo si se traza una recta por este punto, la recta corta al triángulo en dos puntos. Y el punto está entre las dos intersecciones. de la recta con el triángulo
- El interior I de un triángulo es el conjunto de todos sus puntos interiores. I es un conjunto abierto, en el sentido de que para cualquiera de sus puntos P0 el círculo C(P0, r)-los puntos que están a una distancia menor que r están en el interior I.
- El interior unido con el triángulo (como segmentos unidos) es un conjunto cerrado; algunos llaman región triangular , como tal tiene área.
- El triángulo - como unión de segmentos- es, topologimente, frontera de su región triangular.
- Un triangulo es equivalente a un cuadrado, elipse, circunferencia; esto es, se puede establecer una transformación topológica entre dos de tales conjuntos. [7]. De manera que dos puntos próximos en el dominio, siguen próximos en el codominio, se preserva la frontera, el interior, etc, que son propiedades topológicas.
- Una región triangular es un conjunto compacto, pues es cerrado y acotado, inscribible en una circunferencia.
- No es equivalente a una corona circular, pues esta como una región en el plano, tiene su exterior formado por dos conjuntos abiertos y disjuntos. Su exterior no es conjunto conexo, mientras que el exterior de una región triangular sí lo es. Su exterior de la región triangular es abierto y conexo.. [8]
- Tanto un punto cualquiera de la frontera como del interior de un triangulo ( esto es de la región triangular) es un punto de acumulación, pues un círculo abierto centrado en el punto elegido, contiene por lo menos un punto distinto de la región triangular.
Áreas y otras expresiones
Diversas fórmulas del área de una región triangular
Siendo S, el área; a b y c los lados que cumplen x < y+z tambien x-y < z; p = semiperímetro = 0.5 (a+b+c); ha, hb, hc alturas de los lados respectivos; A, B, C medidas de los ángulos interiores opuestos a los lados a,b,c respectivamnete; R radio de la circunferencia circunscrita en torno al triángulo; r, el radio de la circunferencia inscrita en el triángulo; ra, rb, rc, los radios de las circunferencias exinscritas que son tangentes de los lados a,b,c. [9]
- S = 0.5 aha =0.5 b hb= chc; en palabras, el área de la región triangular es el semiproducto de un lado por su altura.
- S = 0.5absenC; semiproducto de dos lados por el seno de ángulo comprendido.
- S = S= abc/4R; el producto de los tres lados entre cuatro veces el radio del la circunferencia circunscrita.
- S = pr = 1/2 (a+ b+ c)r, siendo r el radio de la circunferencia inscrita, a, b, y c los lados del triángulo
- S = ra(p-a); S = rb(p-b); S = rc(p-c);
- S = p(p-a) tag A/2 = p(p-b) tg B/2 = p(p-)tgC/2.
- S = 0.5 a2 sen B sen C ÷ Sen A = 0.5 b2 sen A sen C ÷ Sen B= 0.5 c2 sen B sen A ÷ Sen C, donde a, b y c son lados, y A, B y C, ángulos opuestos. [10]
- S = 2 ×R2 × sen A ×sen B×sen C ; siendo R el radio de la circunferencia circunscrita, A, B y C ángulos del triángulo. [11]
- S = R×r×(senA + senB + senC ); conociendo: R radio de circunferencia circunscrita, r radio de circunfrencia inscrita, A, ,B y C, áncgulos
Fórmula de Molveide
- (a+b)/c = cos[0.5 (A-B)]/ sen (0.5C) = cos[0.5(A-B)]/cos[0.5(A+B)]
- (a-b)/c = sen[0.5 (A-B)]/ cos (0.5C) = sen[0.5(A-B)]/sen[0.5(A+B)]
Líneas en el triángulo
- Mediana
- ma = 0.5 (2b2+2c2-a2)0.5, la mediana que une el vértice A con el punto medio del lado a.
- mb = 0.5 (2a2+2c2-b2)0.5, la mediana que une el vértice B con el punto medio del lado b.
- mc = 0.5 (2b2+2a2-c2)0.5, la mediana que une el vértice C con el punto medio del lado c.
- Altura
- ha = 2[p(p-a)(p-b)(p-c)]0.5 /a, siendo la altura ha, trazada del vértice A a la base a; p es el semiperímetro, p = (a+b+c)/2
- hb = 2[p(p-a)(p-b)(p-c)]0.5 /b, siendo la altura hb, trazada del vértice B a la base b, p el semiperímetro.
- hc = 2[p(p-a)(p-b)(p-c)]0.5 /c, siendo la altura hc, trazada del vértice C a la base c, p el semiperímetro.
- Bisectriz
- wA = 2[bcp(p-a)]0.5 ÷(b+c), corta al lado a, biseca el angBAC:
- wA = 2ab×cosC/2÷ (a+b) = 2ac×cosB/2 ÷ (a+c)
- wB = 2[bcp(p-a)]0.5÷(a+c), corta al lado b, biseca el angABC:
- wB = 2ab×cosC/2: (a+b) = 2ac×cosA/2 ÷ (b+c)
- wC = 2[bcp(p-a)]0.5÷(b+a), corta al lado c, biseca el angACB:
- wC = 2cb×cosA/2:÷(c+b) = 2ac×cosB/2 ÷ (a+c)
Referencias
- ↑ A. V. Pogorélov: Geometría elemental, Editorial Mir, Moscú, 1974
- ↑ A. V. Pogorélov Op. cit.
- ↑ Michael Helfgott: Geometría moderna, Lima
- ↑ Pogorélov. Geometría elemental
- ↑ Elementos de Geometría de G. M. Bruño, editado en Lima, s/f.
- ↑ Bruño: Op. cit.
- ↑ Adaptación de los conceptos de Grupos continuos de Pontriaguin.
- ↑ Salpicones sugerentes en Formas y números de Milton Donaire Peña ISBN 978-612-45279-9-9
- ↑ A. G. Tsipkin, G:G. Tsipkin : Fórmulas matemáticas Álgebra Geometría Análisis Matemático. Editorial Mir, Moscú, 1985; traducido del ruso por Samojválov; impreso en la URSS
- ↑ I. Shariguin: Problemas dfe Geometría, Editorial Mir Moscú 1989
- ↑ I. Shariguin: Op. cit
Fuentes
- Microsoft ® Encarta ® 2007. © 1993--2006 Microsoft Corporation. Reservados todos los derechos.
- Miyares Arturo y Escalona Jose M. Geometría, Segundo Curso. Quinta Edición. Editorial Pueblo y Educación. La Habana. Cuba. 1974.