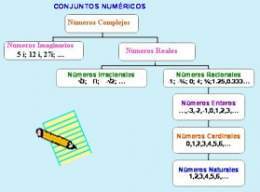
Conjuntos numéricos
| ||||||
Conjuntos numéricos. Son conjuntos de números. En su forma más genérica se refiere a los grandes conjuntos de números como: naturales, enteros, fraccionarios, racionales, irracionales, reales, imaginarios y complejos.
Sumario
Concepto
Los conjuntos numéricos son agrupaciones de números que guardan una serie de propiedades estructurales.
Por ejemplo el sistema más usual en aritmética natural está formado por el conjunto de los números naturales, con la suma, la multiplicación y las relaciones usuales de orden aditivo.
Los conjuntos numéricos son agrupaciones de números que guardan una serie de propiedades estructurales.
Por ejemplo el sistema más usual en aritmética natural está formado por el conjunto de los números naturales, con la suma, la multiplicación y las relaciones usuales de orden aditivo.
Historia
Aunque hoy nos es muy familiar el concepto de número, éste fue elaborado muy lentamente a través de los tiempos. En Mesopotamia, cerca del año 3.000 a. de C, aparecen los primeros vestigios de números naturales, los cuales se anotaban en pequeñas tablillas de barro. A partir del año 1.000 a. de C, se empezó a manejar el concepto de números reales por parte de los egipcios, utilizando fracciones comunes. Esta noción continuó su desarrolló con los aportes de los griegos, que proclamaron la existencia de los números irracionales. A su vez, los números negativos no aparecen sistematizados hasta el año 700 a. de C, en escritos hindúes, evolucionando de mejor manera por los griegos.
Aproximadamente, en el año 600 a. de C, en Grecia, la Escuela de Pitágoras descubrió que no existían dos números naturales m y n, cuyo cociente sea igual a la proporción entre el lado de un cuadrado y su diagonal (números irracionales).
Hacia el año 600 y 500 a. de C, en la India se plasmaron los orígenes de nuestro sistema de numeración, aceptaron las soluciones negativas de las ecuaciones, al tiempo que admitían como números las raíces de otros números que no podían ser expresados mediante números racionales.
Evolución
1) Conjunto de los Números Naturales (N).
N = { 1, 2, 3, 4, 5, 6, 7,.......}
El conjunto de los números naturales surgió de la necesidad de contar, lo cual se manifiesta en el ser humano desde sus inicios.
Este conjunto se caracteriza porque:
- Tiene un número infinito de elementos
- Cada elemento tiene un sucesor y todos, excepto el 1, un antecesor.
- El sucesor de un número natural se obtiene sumando uno (+1); el antecesor se obtiene restando uno (-1).
2) Conjunto de los Números Cardinales (N*).
N* = { 0, 1, 2, 3, 4, 5, 6,.....}
Al Conjunto de los números naturales se le agregó el 0 (cero) y se forma el Conjunto de los Números Cardinales.
3) Conjunto de los números fraccionarios (Q+)
Q+ = { 0, ½ , 2, 3/4 3, 9/7,.....}
Los números fraccionarios son aquellos que se expresan de las forma o como una expresión decimal periódica.
4) Conjunto de los Números Enteros (Z).
Z = { ..... –3, -2, -1, 0, 1, 2, 3,...}
El Conjunto de los números enteros surge de la necesidad de dar solución general a la sustracción, pues cuando el sustraendo es mayor que el minuendo, esta sustracción no tiene solución en los Conjuntos Naturales y Cardinales (por ejemplo: 5 – 20 = ¿?).
Debido a esto, la recta numérica se extiende hacia la izquierda, de modo que a cada punto que representa un número natural le corresponda un punto simétrico, situado a la izquierda del cero. Punto simétrico es aquel que está ubicado a igual distancia del cero (uno a la derecha y el otro a la izquierda de él).
Z = N* U Conjunto de los Números Enteros negativos.
Z = Tiene 3 Subconjuntos:
- Enteros Negativos: Z ¯
- Enteros Positivos: Z +
- Enteros Positivos y el Cero: Z+ U {0}
Por lo tanto, el Conjunto de los números enteros es la unión de los tres subconjuntos mencionados.
Z = Z - U {0} U Z +
5) Conjunto de los Números Racionales Q.
Q = {....- ¾, - ½, - ¼ , 0, ¼ , ½, ¾,.....}
El conjunto de los números racionales se creó debido a las limitaciones de cálculo que se presentaban en el conjunto de los números naturales, números cardinales y números enteros.
Por ejemplo, sólo se puede dividir en el conjunto de los números enteros si y sólo si el dividendo es múltiplo, distinto de cero, del divisor. Para solucionar esta dificultad, se creó este conjunto, el cual está formado por todos los números de la forma a/b. Esta fracción en la cual el numerador es a, es un número entero y el denominador b, es un número entero distinto de cero.
El conjunto de los números racionales (Q ) se ha construido a partir del conjunto de los números enteros (Z).
Se expresa por comprensión como: Q = { a /b tal que a y b€ Z; y b≠ 0 }
Este conjunto se representa gráficamente, dividiendo cada intervalo de una recta numérica en espacios iguales, que representen números enteros. Cada una de estas subdivisiones representa una fracción con denominador igual al número de partes de la subdivisión.
Cada fracción es un número racional y cada número racional consta de infinitas fracciones equivalentes.
6) Conjunto de Números Irracionales (I).
I = Conjunto de Números Decimales Infinitos no Periódicos.
Este conjunto surgió de la necesidad de reunir a ciertos números que no pertenecen a los conjuntos anteriores; entre ellos se pueden citar a las raíces inexactas, el número Pi, etc. A él pertenecen todos los números decimales infinitos puros, es decir aquellos números que no pueden transformarse en una fracción. No deben confundirse con los números racionales, porque éstos son números decimales finitos, infinitos periódicos e infinitos semiperiódicos que sí pueden transformarse en una fracción.
Ejemplos: 1,4142135....
0,10200300004000005....
7) Conjunto de Números Reales (R).
R = {....- 10, -1, - ¾, - ½, - ¼, 0, ¼ , √2, 5 , .....}
Se denotan por R. R= {Q U irracionales}.
8) Conjunto de Números Imaginarios (i)
Surgen por la necesidad de obtener las raíces de índice par de cantidades negativas. Se denotan por i. La unidad de los números imaginarios es la raíz cuadrada de – 1 y se denota por i, así que: i = √-1.
Debes tener en cuenta:
i2 = -1, i 3 = - i, i 4 = 1.
9) Conjunto de Números Complejos (C)
La unión de los números reales con los imaginarios da origen a los números complejos denotados por C.
Características estructurales
Sus características estructurales más importantes son:
- No son conjuntos finitos.
- Dotados de operadores, admiten estructura algebraica estable.
- Están dotados de propiedades topológicas (o pueden llegar a estarlo).
- Admiten relación de orden.
- Admiten relación de equivalencia.
- Son representables mediante diagramas de Hasse, diagramas de Euler y diagramas de Venn, pudiéndose tomar una combinación de ambos en un diagrama de Euler-Venn con la forma característica de cuadrilátero y además pudiéndose representar internamente un diagrama de Hasse (es una recta).
- Todos los conjuntos numéricos se construyen desde una estructura más simple hasta otra más compleja.
- El orden de construcción de los conjuntos numéricos (de menor a mayor complejidad) es el siguiente:
N: Conjunto de los números naturales
Q+: Conjunto de los números fraccionarios
Z: Conjunto de los números enteros
Q: Conjunto de los números racionales
I: Conjunto de los números irrracional
R: Conjunto de los números reales
C: Conjunto de los números complejos
- Todos los conjuntos numéricos son a su vez, subconjuntos del Conjunto de los números complejos.
- El conjunto de los conjuntos numéricos es representable a través del Diagrama del Dominó o de Llaves.
Formas de representación
Los conjuntos numéricos se pueden representar:
- Mediante una definición intensiva, usando una regla o definición semántica: A es el conjunto cuyos elementos son todos los números impares menores que 20.
- Por extensión, listando cada miembro del conjunto. En una definición extensiva se escriben los elementos del conjunto entre llaves: C = {1,3, 5, 7, 9, 11, 13, 15, 17, 19}
- Por comprensión: escribiendo dentro de una llave una propiedad característica de los elementos del conjunto y solamente de ellos. F = {n2: n es un entero y 1 ≤ n ≤ 10},donde en esta expresión los dos puntos (":") significan "tal que". Así, el conjunto anterior es el conjunto de "los números de la forma n2 tal que n es un número natural entre 1 y 10 (ambos inclusive)", o sea, el conjunto de los once primeros cuadrados de números naturales, {1, 4, 9, 16, 25, 36, 49, 64, 81, 100}. En lugar de los dos puntos se utiliza también la barra vertical ("|").
- Por intervalos.
Fuentes
- Cuaderno complementario. Matemática 8vo grado
- Libro de texto. Matemática 7mo grado
- Libro de texto. Matemática 10mo grado