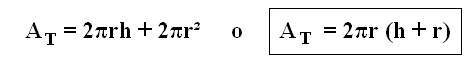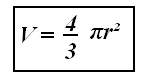Cuerpos de revolución
| ||||||
Cuerpos de revolución. Cuerpo obtenido a partir del giro de una figura plana alrededor de un eje. Los tres cuerpos de revolución más importantes son el cilindro, el cono y la
esfera.
La observación de la naturaleza nos muestra la existencia de variadas formas en los cuerpos materiales que la componen y nos proporciona la idea de volumen, superficie, línea, y punto.
Por necesidades prácticas, el desarrollo de técnicas usadas para medir, construir o desplazarse, llevaron al hombre a hacer uso de las diversas propiedades de las figuras geométricas y, en muchos casos a formar
“cuerpos” a partir de estas.
Sumario
Reseña histórica
La Geometría es una de las más antiguas ciencias. Inicialmente, constituía un cuerpo de conocimientos prácticos en relación con las longitudes, áreas y volúmenes. En el Antiguo Egipto estaba muy desarrollada, según los textos de Heródoto, Estrabón y Diodoro Sículo.
Una vez adquiridas estas nociones y prescindiendo de su origen práctico, la Geometría (medición de la Tierra), de ser un conjunto de técnicas, pasó a constituir una disciplina matemática formal, donde la figura geométrica es un ente abstracto y sus propiedades el objeto de estudio de la Geometría.
Cilindro
Definición y elementos
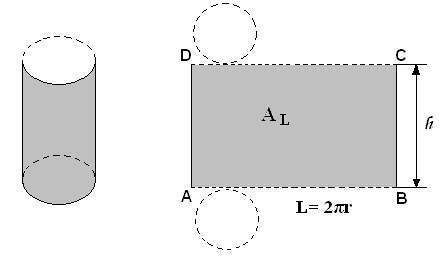
El cilindro es el cuerpo que se obtiene a partir de un rectángulo que gira alrededor de uno de sus lados.
Cálculo del área
Si se desarrolla la superficie lateral del cilindro de radio r y de altura h, se obtiene una superficie plana que es un rectángulo.
El largo del rectángulo es igual a la longitud de las circunferencias que limitan las bases
( L= 2πr ) y su altura es igual a la altura del cilindro.
Por tanto el área lateral (AL) del cilindro es igual al área del rectángulo ABCD obtenido.
El área total (AT) del cilindro es igual a la suma del área lateral y las de sus dos bases.
Sustituyendo
Se obtiene:
Y es de esta forma que se puede hallar el área del cilindro.
Cálculo del volumen
El volumen de un prisma es igual al producto del área de la base por la altura:
Esta misma fórmula es la que se utiliza para calcular el volumen de un cilindro.
Cono
Definición y elementos
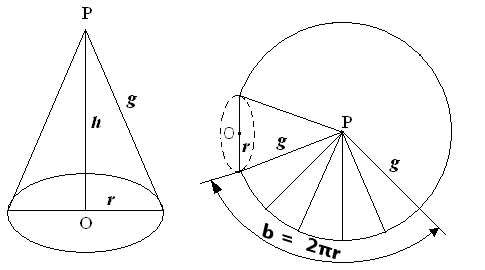
El cono es el cuerpo obtenido de un triángulo rectángulo que gira alrededor de uno de sus catetos.
Área del cono
Si se desarrolla la superficie lateral del cono de radio r, generatriz g y altura h, se obtiene una superficie plana que es un sector circular de radio g, determinado por un arco b cuya longitud es igual a la longitud de la circunferencia de la base: b = 2πr.
Por tanto:
El área lateral del cono es igual al área del sector circular así obtenido. El área del sector circular se calcula utilizando la proporción siguiente:
Sustituyendo en (1)
El área total del cono circular recto es igual a la suma del área lateral y el área de su base.
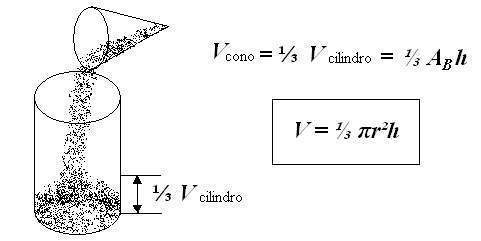
Cálculo de su volumen
La relación que existe entre los volúmenes de un prisma y el de una pirámide que tengan iguales las bases y la altura, es la misma que existe entre los volúmenes de un cilindro y un cono que cumplan estas mismas condiciones.
O sea: el volumen de un cono de radio r y altura h es igual a la tercera parte del volumen del cilindro de igual radio y altura.
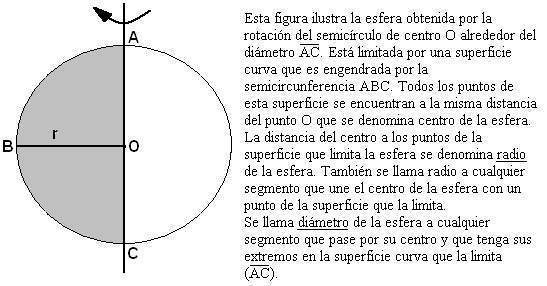
Esfera
Definición y elementos
La esfera es el cuerpo que se obtiene a partir de un semicírculo que gira alrededor de su diámetro.
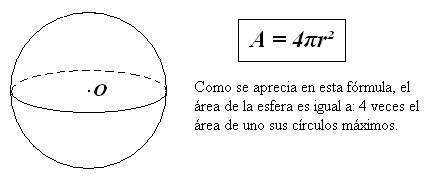
Cálculo del área de una esfera
El área de una esfera de radio r es el área de la superficie curva que la limita:
Volumen de la esfera
El volumen de una esfera de radio r es:
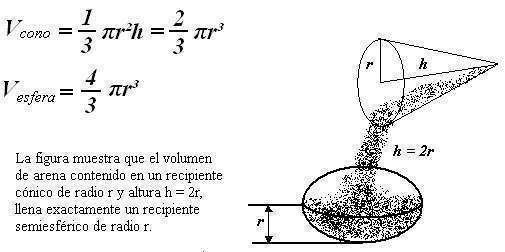
Se puede comprobar experimentalmente que el volumen de un cono de radio r y la altura h con h = 2r, es igual a la mitad del volumen de la esfera del mismo radio.
Fuente
- Libro de texto de Matemática, 8vo grado. Editorial Pueblo y Educación, 1990.