Igualdad de triángulos
| ||||||
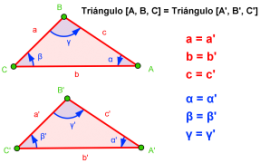
Igualdad de triángulos. Dos triángulos que tienen todos sus lados y ángulos respectivamente congruentes (iguales).
Sumario
Triángulos
Un triángulo es un polígono de tres lados, por tanto, tiene tres vértices y tres ángulos.
Nomenclatura:
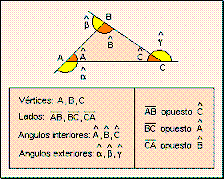
- En un triángulo, la letra que se usa para el vértice es mayúscula: A,B,C.
- Las mismas letras mayúsculas, con un "sombrero", para nombrar el ángulo: Â,B,Ĉ, aunque también son usuales las letras griegas: α, β, λ
- El nombre de cada lado se expresa con una letra minúscula: a, b, c; es la letra correspondiente al vértice opuesto al lado. También se puede expresar cada lado con dos letras mayúsculas: BC, AC, AB, las de los vértices contenidos en ese lado.
Propiedades de los triángulos
- La suma de los ángulos interiores es de 180º.
- La longitud de cada lado, es menor, que la suma de los otros dos.
- Es rígido, de hecho, es el único polígono indeformable.
Igualdad de triángulos
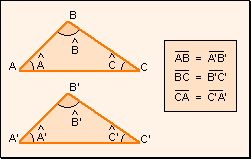
Dos triángulos son iguales si “podemos superponer uno sobre el otro” obteniéndose figuras coincidentes. En términos de los elementos que componen un triángulo, este concepto puede expresarse de la siguiente forma:
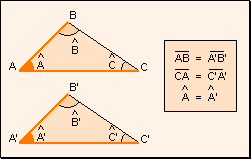
Definición Dos triángulos son iguales si tienen los lados y los ángulos iguales dos a dos. Si dos triángulos ABC y A0B0C0 son iguales, se escribirá ABC = A0B0C0.
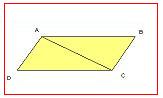
Ejemplo. Sea ABCD un paralelogramo en el que se ha trazado una de sus diagonales:
Los triángulos ADC y ABC son iguales. Atendiendo a la definición, se debe comprobar que los lados y los ángulos coinciden dos a dos. En primer lugar, el lado AC es común a ambos triángulos. Por otra parte, por ser ABCD un paralelogramo, los lados paralelos son iguales dos a dos, esto revela que
DC (en ADC) = AB (en ABC)
AD (en ADC) = BC (en ABC)
Se tiene la igualdad de los lados. A continuación, se demostrará la igualdad entre ángulos.
Por ser ABCD un paralelogramo, los ángulos opuestos son iguales, esto permite afirmar que ˆD = ˆB (o, si se prefiere, < ADC =< ABC). Para los otros ángulos, obsérvese que los lados AD y BC son paralelos y la diagonal AC corta a ambos, por la propiedad de ángulos alternos–internos se verifica:
Aˆ (en ADC) = Cˆ (en ABC)
Cˆ (en ADC) = Aˆ (en ABC)
Criterios de igualdad de triángulos
Dos triángulos son iguales si se cumple alguno de los siguientes criterios:
- Tienen los lados iguales dos a dos.
- Tienen iguales dos lados y el ángulo comprendido.
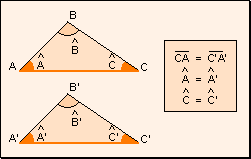
- Tienen iguales un lado y los dos ángulos adyacentes.
- Tienen dos lados y el ángulo opuesto al lado mayor respectivamente iguales.
Según los criterios anteriores, dos triángulos son iguales si en ellos podemos observar tres elementos iguales, siendo uno de estos elementos un lado: en cualquier caso, a la hora de comprobar que dos triángulos cualesquiera son iguales, se aplicará alguno de los tres criterios (dependiendo de los datos que se tengan) pues exigen menos trabajo que la definición de igualdad de triángulos.
Propiedades de la igualdad de triángulos
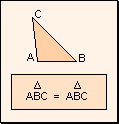
- Carácter reflexivo: Todo triángulo es igual a si mismo.
- Carácter simétrico: Si un triángulo es igual a otro, éste es igual a primero.
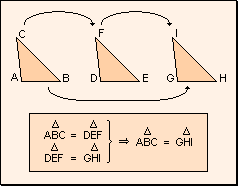
- Carácter transitivo: Si un triángulo es igual a otro y éste es igual a un tercero, el primero es igual al tercero.
Fuentes
- Artículo Igualdad de triángulos. Disponible en ¨es.wikipedia.org¨. Consultado el 15 de marzo del 2011.
- Artículo Criterios de igualdad. Disponible en ¨www.kalipedia.com¨. Consultado el 15 de marzo del 2011.