Diferencia entre revisiones de «Cubo»
(→Fuentes) |
|||
| (No se muestran 10 ediciones intermedias de 5 usuarios) | |||
| Línea 1: | Línea 1: | ||
| − | + | ||
| − | {{Definición|Nombre=Cubo|imagen=Cubo_plantilla.JPG|concepto=Sólido regular limitado por seis [[Cuadrado|cuadrados]] iguales.}} | + | {{Definición|Nombre=Cubo |
| − | + | |imagen=Cubo_plantilla.JPG | |
| − | '''Cubo(Figura)'''. Es un [[Poliedro]] regular limitado por seis [[Cuadrado|cuadrados]] iguales. También se le conoce con el nombre de hexaedro regular, o simplemente hexaedro. | + | |concepto=Sólido regular limitado por seis [[Cuadrado|cuadrados]] iguales. |
| − | + | }} | |
| − | == Descripción == | + | |
| + | '''Cubo (Figura)'''. Es un [[Poliedro]] regular limitado por seis [[Cuadrado|cuadrados]] iguales. También se le conoce con el nombre de hexaedro regular, o simplemente hexaedro. | ||
| + | |||
| + | == Descripción == | ||
El cubo es un [[Ortoedro|ortoedro]], es decir, tiene sus seis caras rectas y perpendiculares entre sí. Además de ser sus caras [[Rectángulo|rectángulos]], también son [[Cuadrado|cuadrados]]. | El cubo es un [[Ortoedro|ortoedro]], es decir, tiene sus seis caras rectas y perpendiculares entre sí. Además de ser sus caras [[Rectángulo|rectángulos]], también son [[Cuadrado|cuadrados]]. | ||
| Línea 15: | Línea 18: | ||
*Número de aristas desde un vértice: 3<br> | *Número de aristas desde un vértice: 3<br> | ||
| − | == Área == | + | == Área == |
| − | === Área | + | === Área lateral === |
| − | El área lateral(A<sub>L</sub>), se calcula como la suma de las áreas de las cuatro caras laterales | + | El área lateral(A<sub>L</sub>), se calcula como la suma de las áreas de las cuatro caras laterales; formadas por [[Cuadrado|cuadrados]], y teniendo como premisa que todas las caras del cubo son iguales, entonces podemos hallar el área de una de ellas, y multiplicarla por 4. Siendo '''a''' la longitud de la arista del cubo, entonces su área( A<sub>L</sub>) se expresa mediante la fórmula: A<sub>L</sub>= 4 * a<sup>2</sup> |
| − | === Área | + | === Área total === |
| − | El área total(A<sub>T | + | El área total(A<sub>T</sub>), se calcula como el '''A<sub>L</sub>''' más el área de los otros dos [[Cuadrado|cuadrados]] iguales a los anteriores que conforman las bases superior e inferior, es decir, que a diferencia del A<sub>L</sub> que se multiplica por cuatro, el área total A<sub>T</sub> incluye otros dos, lo que equivale a que el área total (A<sub>T</sub>), se calcule a través de la fórmula: A<sub>T</sub> = 6 * a<sup>2</sup><br> |
| − | == Volumen == | + | == Volumen == |
Siendo a la longitud de la arista del cubo, entonces su Volumen ( V) se expresa mediante la fórmula: V= a<sup>3</sup> | Siendo a la longitud de la arista del cubo, entonces su Volumen ( V) se expresa mediante la fórmula: V= a<sup>3</sup> | ||
| − | == Diagonales == | + | == Diagonales == |
| − | === Diagonal de la base === | + | === Diagonal de la base === |
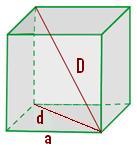
| − | [[Image: | + | [[Image:Cubo diagonal.JPG|thumb|right|Diagonales del Cubo]]La diagonal '''d''' de la base (o cualquiera de sus caras), partiendo de que '''a''' es la longitud de la arista del cubo, se calcula a través de la fórmula: [[Image:Cubo diagbase form.JPG]] |
| − | === Diagonal del Cubo === | + | === Diagonal del Cubo === |
| − | La diagonal '''D''' del cubo, es el segmento que une dos vértices de caras opuestas, y que no pertenezcan a un mismo plano que contenga alguna de las caras del cubo. Tomando a '''a''' como arista del cubo, se calcula a través de la fórmula: [[Image: | + | La diagonal '''D''' del cubo, es el segmento que une dos vértices de caras opuestas, y que no pertenezcan a un mismo plano que contenga alguna de las caras del cubo. Tomando a '''a''' como arista del cubo, se calcula a través de la fórmula: [[Image:Cubo diagonal form.JPG]] |
| − | == Desarrollo == | + | == Desarrollo == |
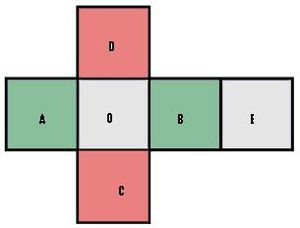
| − | Si desea armar un cubo con [[Papel|papel]], u otro material, se consigue de una manera muy sencilla, proceda a construirlo como se explica a continuación. Distribuya 6 [[Cuadrado|cuadrados]] iguales como se muestra en la figura, y seguidamente doble los cuadrados '''A, B, C, D''', sobre el cuadrado '''O'''. Seguidamente, doble el cuadrado '''E''' de manera que descanse sobre los demás cuadros. Por último proceda a unir de alguna manera los bordes de los cuadrados que quedaron unidos, y ya tiene el cubo armado. | + | [[Image:Cubo desarrollo.JPG|thumb|right|Desarrollo del Cubo]]Si desea armar un cubo con [[Papel|papel]], u otro material, se consigue de una manera muy sencilla, proceda a construirlo como se explica a continuación. Distribuya 6 [[Cuadrado|cuadrados]] iguales como se muestra en la figura, y seguidamente doble los cuadrados '''A, B, C, D''', sobre el cuadrado '''O'''. Seguidamente, doble el cuadrado '''E''' de manera que descanse sobre los demás cuadros. Por último proceda a unir de alguna manera los bordes de los cuadrados que quedaron unidos, y ya tiene el cubo armado. |
== Véase también == | == Véase también == | ||
| Línea 58: | Línea 61: | ||
== Fuentes == | == Fuentes == | ||
| − | *[http://www.bbo.arrakis.es/geom/cubo1.htm Cubo] | + | *[http://www.bbo.arrakis.es/geom/ cubo1.htm Cubo] |
| − | *[http://es.wikipedia.org/wiki/Cubo Cubo] | + | |
| − | *[http://www.vitutor.net/2/2/15.html Vitutor] | + | *[http://es.wikipedia.org/wiki/ Cubo Cubo] |
| − | *Miyares Arturo y Jose M Escalona. [[Geometría]], Segundo Curso. Quinta Edición. Editorial Pueblo y Educación. [[La | + | |
| − | + | *[http://www.vitutor.net/2/2/15.html Vitutor] | |
| − | [[ | + | |
| + | *Miyares Arturo y Jose M Escalona. [[Geometría]], Segundo Curso. Quinta Edición. Editorial Pueblo y Educación. [[La Habana]]. [[Cuba]]. [[1974|1974]]. | ||
| + | |||
| + | [[Categoría:Figuras geométricas]] | ||
| + | [[Categoría:Volumen]] | ||
| + | [[Categoría:Geometría elemental]] | ||
última versión al 15:28 3 ago 2024
| ||||||
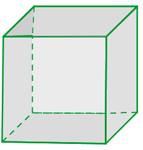
Cubo (Figura). Es un Poliedro regular limitado por seis cuadrados iguales. También se le conoce con el nombre de hexaedro regular, o simplemente hexaedro.
Sumario
Descripción
El cubo es un ortoedro, es decir, tiene sus seis caras rectas y perpendiculares entre sí. Además de ser sus caras rectángulos, también son cuadrados.
Tiene las siguientes propiedades:
- Número de caras: 6
- Número de vértices: 6
- Número de aristas: 12
- Número de aristas desde un vértice: 3
Área
Área lateral
El área lateral(AL), se calcula como la suma de las áreas de las cuatro caras laterales; formadas por cuadrados, y teniendo como premisa que todas las caras del cubo son iguales, entonces podemos hallar el área de una de ellas, y multiplicarla por 4. Siendo a la longitud de la arista del cubo, entonces su área( AL) se expresa mediante la fórmula: AL= 4 * a2
Área total
El área total(AT), se calcula como el AL más el área de los otros dos cuadrados iguales a los anteriores que conforman las bases superior e inferior, es decir, que a diferencia del AL que se multiplica por cuatro, el área total AT incluye otros dos, lo que equivale a que el área total (AT), se calcule a través de la fórmula: AT = 6 * a2
Volumen
Siendo a la longitud de la arista del cubo, entonces su Volumen ( V) se expresa mediante la fórmula: V= a3
Diagonales
Diagonal de la base
La diagonal d de la base (o cualquiera de sus caras), partiendo de que a es la longitud de la arista del cubo, se calcula a través de la fórmula:
Diagonal del Cubo
La diagonal D del cubo, es el segmento que une dos vértices de caras opuestas, y que no pertenezcan a un mismo plano que contenga alguna de las caras del cubo. Tomando a a como arista del cubo, se calcula a través de la fórmula:
Desarrollo
Si desea armar un cubo con papel, u otro material, se consigue de una manera muy sencilla, proceda a construirlo como se explica a continuación. Distribuya 6 cuadrados iguales como se muestra en la figura, y seguidamente doble los cuadrados A, B, C, D, sobre el cuadrado O. Seguidamente, doble el cuadrado E de manera que descanse sobre los demás cuadros. Por último proceda a unir de alguna manera los bordes de los cuadrados que quedaron unidos, y ya tiene el cubo armado.
Véase también
- Triángulo
- Cuadrado
- Paralelogramo
- Rectángulo
- Trapecio
- Circunferencia
- Círculo
- Cuadrilátero
- Pirámide
- Ortoedro