Cuadrilátero
| ||||||
Cuadrilátero (Figura). Los cuadriláteros son los polígonos que tienen cuatro lados. Si te fijas, cerca de ti hay muchos objetos cuyo contorno es como el de un cuadrilátero: una ventana, la pantalla de una computadora o de un televisor plano, un póster, una puerta o el trapecio que forma en el suelo la luz del Sol que entra por la ventana. Los cuadriláteros son los polígonos que más abundan a nuestro alrededor, más que los triángulos y, por supuesto, que los pentágonos, hexágonos, etc.
Sumario
Área
Como en los cuadriláteros de forma general, puede variar la naturaleza de sus elementos (ángulos, lados, diagonales, etc.), es decir, el comportamiento de los mismos, se recomienda dividirlo en figuras conocidas, como triángulos y / o rectángulos, etc., según lo permita, hallar el área de estas figuras conocidas, y por último, hallar la suma de estas áreas. A esta suma total se le denomina área del cuadrilátero.
Perímetro
El perímetro (p) del cuadrilátero se calcula sumando las longitudes de los cuatro lados del cuadrilátero. Es decir, si denominamos a, b, c, y d, las longitudes de estos lados, podemos calcular el perímetro a través de la siguiente fórmula: A = a + b + c + d.
Clasificación
Los cuadriláteros de forma general se clasifican en dos grandes grupos:
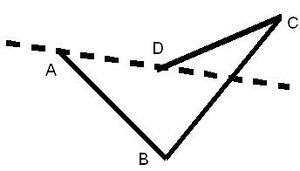
Complejos ( inconexos) y simples. Los primeros, conocidos como cuadriláteros autosecantes, se caracterizan porque dos de sus lados, no consecutivos, se cortan entre sí. Su figura es la unión de dos regiones triangulares con un vértice común. En los cuadriláteros simples cada lado tiene un solo punto común ( vértice) con uno de los dos lados, que le precede o le sigue [1]
Los simples se clasifican en:
- Cóncavos: Son aquellos cuadriláteros, que al menos uno de sus lados cumple la condición de que la línea que lo contiene, divide a la figura en dos partes, o sea, la deja en ambos semiplanos en que divide la línea al plano.
- Convexos: Son aquellos cuadriláteros que cumplen la condición de que al prolongar cualquiera de sus lados, la línea que lo contiene deja al cuadrilátero en un solo semiplano.
Subclases de los cudriláteros convexos
Los cuadriláteros cóncavos no son de relevancia para el estudio en la escuela. Por esa razón en este artículo se hablará de los cuadriláteros convexos. Estos se clasifican en Paralelogramos, Trapecios y Trapezoides.
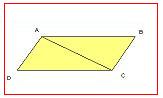
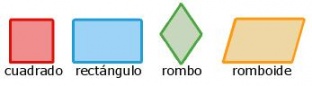
Paralelogramos: Tienen sus dos pares de lados opuestos paralelos. en estos se incluyen el Cuadrado, Rectángulo, Rombo y Romboide.
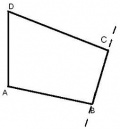
Trapecios: Tienen un solo par de lados paralelos. Dentro de ellos está el isósceles y el escaleno.
Trapezoides: No tienen ningún lado paralelo a su lado opuesto.
Definición directa
Los cuadriláteros más conocidos y los más utilizados, tanto en los estudios teóricos como en aplicaciones de uso social y técnico, los podemos definir considerando como cuadriláteros con características propias bien definidas.
- Trapecio
Cuadrilátero sólo un par de lados paralelos .
- Rombo
Cuadrilátero con los cuatro lados iguales.
- Rectángulo
Cuadrilátero con cuatro ángulos rectos.
- Cuadrado
Un cuadrilátero equilátero y equiángulo.
Propiedades
- La suma de los cuatro ángulos interiores equivale a cuatro rectos.
- Tiene dos diagonales en total, y desde un vértice se puede trazar solo una.
- Las diagonales de los convexos se cortan en un punto interior del cuadrilátero.
- Las diagonales de un cuadrilátero cóncavo no se cortan; pues una está en el interior y la otra está en el exterior.
Construcción de un cuadriátero convexo
- Para construir un triángulo cualquiera es suficiente conocer tres lados, teniendo en cuenta que la suma de las longitudes de dos de ellos sea mayor que la del tercer lado. Sin embargo, en el caso de un cuadrilátero convexo no son suficientes disponer de la la existencia de cuatro lados. Necesariamente hay que conocer, por lo menos, un ángulo y como datos mínimos conocer dos lados.
- Siempre que se conozcan los cuatro lados y una diagonal. Caso que se reduce a la construcción de dos triángulos con un lado común( la diagonal). La reunión de estos dos triángulos da el cuadrilátero buscado.
- Cuando se conocen un lado, los ángulos adyacentes a este lado, y sendos lados de distinta longitud que parten de los extremos del primer lado. Los ángulos propuestos no pueden exceder separadamente, en medida 180º.
- Otro caso en la situación de conocer dos lados consecutivos y tres ángulos consecutivos, uno de estos formado por los lados propuestos y los otros ángulos tienen su vértice en cada extremo no común de los lados. [2]
Véase también
- Triángulo
- Cuadrado
- Paralelogramo
- Rombo
- Rectángulo
- Circunferencia
- Círculo
- Trapecio
- Wikipedia en ruso
Referencias
Fuentes
- Microsoft ® Encarta ® 2007. © 1993--2006 Microsoft Corporation. Reservados todos los derechos.
- Miyares Arturo y Jose M Escalona. Geometría, Segundo Curso. Quinta Edición. Editorial Pueblo y Educación. La Habana. Cuba. 1974.