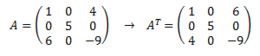Diferencia entre revisiones de «Matriz traspuesta»
(Nuevo artículo) |
m (Texto reemplazado: «<div align="justify">» por «») |
||
| (No se muestran 2 ediciones intermedias de otro usuario) | |||
| Línea 1: | Línea 1: | ||
{{Definición|Nombre=Matriz traspuesta|imagen=Matriz_traspuesta.png|concepto=[[Matriz]] que se obtiene al cambiar las filas de una matriz por las columnas.}} | {{Definición|Nombre=Matriz traspuesta|imagen=Matriz_traspuesta.png|concepto=[[Matriz]] que se obtiene al cambiar las filas de una matriz por las columnas.}} | ||
| − | + | ||
'''Matriz traspuesta'''. Dícese de la [[matriz]] que se obtiene al cambiar las filas por las columnas. | '''Matriz traspuesta'''. Dícese de la [[matriz]] que se obtiene al cambiar las filas por las columnas. | ||
| Línea 17: | Línea 17: | ||
*La traspuesta de la suma es la suma de las traspuestas: (A+B)<sup>T</sup> = A<sup>T</sup>+B<sup>T</sup> | *La traspuesta de la suma es la suma de las traspuestas: (A+B)<sup>T</sup> = A<sup>T</sup>+B<sup>T</sup> | ||
*Traspuesta del producto: (A·B)<sup>T</sup> = B<sup>T</sup>·A<sup>T</sup> | *Traspuesta del producto: (A·B)<sup>T</sup> = B<sup>T</sup>·A<sup>T</sup> | ||
| − | *Una matriz es igual que su traspuesta si, y sólo si, es simétrica. | + | *Una matriz es igual que su traspuesta si, y sólo si, es una [[Matriz simétrica|matriz simétrica]]. |
| − | *La traspuesta de una matriz diagonal y cuadrada ''A'' es ''A''. La igualdad no es cierta si la matriz es diagonal pero no cuadrada. | + | *La traspuesta de una matriz diagonal y cuadrada ''A'' es ''A''. La igualdad no es cierta si la matriz es [[Matriz diagonal|diagonal]] pero no cuadrada. |
*El determinante de una matriz regular es igual al de su traspuesta. | *El determinante de una matriz regular es igual al de su traspuesta. | ||
| − | |||
==Véase también== | ==Véase también== | ||
* [[Matriz diagonal]] | * [[Matriz diagonal]] | ||
| + | *[[Matriz simétrica]] | ||
*[[Matriz Hessenberg]] | *[[Matriz Hessenberg]] | ||
*[[Matriz regular]] | *[[Matriz regular]] | ||
última versión al 21:38 12 ago 2019
| ||||||
Matriz traspuesta. Dícese de la matriz que se obtiene al cambiar las filas por las columnas.
Definición
Sea A una matriz de orden mxn, se define su matriz traspuesta como la matriz de dimensión nxm que resulta al cambiar las filas de A por las columnas de A. La matriz traspuesta de A se denota por AT ó por A'.
Obsérvese que el elemento de la fila i y columna j de A es el elemento de la fila j y columna i de AT.
Ejemplo: la matriz traspuesta de la matriz identidad es igual a la propia matriz.
Propiedades
- La matriz traspuesta de la matriz traspuesta de A es A: (AT)T = A
- La traspuesta de la suma es la suma de las traspuestas: (A+B)T = AT+BT
- Traspuesta del producto: (A·B)T = BT·AT
- Una matriz es igual que su traspuesta si, y sólo si, es una matriz simétrica.
- La traspuesta de una matriz diagonal y cuadrada A es A. La igualdad no es cierta si la matriz es diagonal pero no cuadrada.
- El determinante de una matriz regular es igual al de su traspuesta.