Diferencia entre revisiones de «Matriz Hessenberg»
(Nuevo artículo) |
m (Texto reemplazado: «<div align="justify">» por «») |
||
| Línea 1: | Línea 1: | ||
{{Definición|Nombre=Matriz Hesenberg|imagen=Matriz_Hessenberg_Superior.png|Cconcepto=[[Matriz]] Hessenberg superior: todos los elementos por debajo de la diagonal -1 son nulos.}} | {{Definición|Nombre=Matriz Hesenberg|imagen=Matriz_Hessenberg_Superior.png|Cconcepto=[[Matriz]] Hessenberg superior: todos los elementos por debajo de la diagonal -1 son nulos.}} | ||
| − | + | ||
'''Matriz Hessenberg'''. Dícese de una [[matriz]] cuadrada cuyos elementos por encima (o por debajo) de la diagonal -1 son negativos. | '''Matriz Hessenberg'''. Dícese de una [[matriz]] cuadrada cuyos elementos por encima (o por debajo) de la diagonal -1 son negativos. | ||
última versión al 22:42 12 ago 2019
| ||||
Matriz Hessenberg. Dícese de una matriz cuadrada cuyos elementos por encima (o por debajo) de la diagonal -1 son negativos.
Definición
Sea A una matriz cuadrada,
- es una matriz Hessenberg superior si todos los elementos por debajo de la diagonal -1 son nulos. Ejemplo:
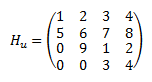
- es una matriz Hessenberg inferior si todos los elementos por encima de la diagonal -1 son nulos. Ejemplo:
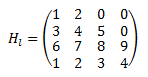
Propiedades
- No toda matriz Hessenberg es triangular.
- Una matriz triangular superior es Hessenberg superior.
- Una matriz triangular inferior es Hessenberg inferior.
- El producto de una matriz de Hessenberg con una matriz triangular es otra matriz de Hessenberg.
- Si A es una matriz superior de Hessenberg y T es una matriz triangular superior, entonces A·T y T·A son matrices superiores de Hessenberg.