Diferencia entre revisiones de «Integral Indefinida»
(→Métodos de integración) |
m (Texto reemplazado: «<div align="justify">» por «») |
||
| (No se muestran 3 ediciones intermedias de otro usuario) | |||
| Línea 5: | Línea 5: | ||
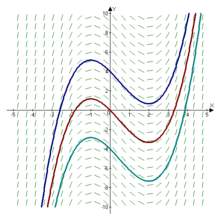
|concepto= El [http://es.wikipedia.org/wiki/Campo_vectorial campo vectorial] definido asignando a cada punto (x, y) un [[Vectores_Polares_y_Vectores_Axiales|vector]] que tiene por pendiente ƒ(x) = (x<sup>3</sup>/3)-(x<sup>2</sup>/2)-x. Se muestran tres de las infinitas primitivas de ƒ(x) que se pueden obtener variando la constante de integración C. | |concepto= El [http://es.wikipedia.org/wiki/Campo_vectorial campo vectorial] definido asignando a cada punto (x, y) un [[Vectores_Polares_y_Vectores_Axiales|vector]] que tiene por pendiente ƒ(x) = (x<sup>3</sup>/3)-(x<sup>2</sup>/2)-x. Se muestran tres de las infinitas primitivas de ƒ(x) que se pueden obtener variando la constante de integración C. | ||
}} | }} | ||
| − | + | ||
'''Integral indefinida'''. Es el conjunto de las infinitas [http://www.mitecnologico.com/Main/DefinicionFuncionPrimitiva primitivas] que puede tener una [[función|función]]. | '''Integral indefinida'''. Es el conjunto de las infinitas [http://www.mitecnologico.com/Main/DefinicionFuncionPrimitiva primitivas] que puede tener una [[función|función]]. | ||
| Línea 73: | Línea 73: | ||
=== Ejemplos === | === Ejemplos === | ||
| + | |||
* [[Image:EjempIntegral1.gif]] | * [[Image:EjempIntegral1.gif]] | ||
| Línea 82: | Línea 83: | ||
Así, dada una función f(x), los métodos de integración son técnicas cuyo uso (usualmente combinado) permite encontrar una función F(x) tal que | Así, dada una función f(x), los métodos de integración son técnicas cuyo uso (usualmente combinado) permite encontrar una función F(x) tal que | ||
| − | F(x)=∫ ƒ(x) dx | + | |
| − | lo cual, por el teorema fundamental del cálculo equivale a hallar una función F(x) tal que f(x) es su derivada | + | <big>F(x)=∫ ƒ(x) dx</big> |
| + | |||
| + | lo cual, por el teorema fundamental del cálculo equivale a hallar una función F(x) tal que f(x) es su [[Derivada_de_una_función|derivada]]. | ||
| + | |||
[[Image:Defmetintegracion.png]] | [[Image:Defmetintegracion.png]] | ||
| − | |||
Existen varios métodos entre los que se destacan los siguientes: | Existen varios métodos entre los que se destacan los siguientes: | ||
| − | * [[Integración por Cambio de variable]]. | + | * [[Integración_por_el_método_cambio_de_variable|Integración por Cambio de variable]]. |
| − | * [[Integración por | + | * [[Integración por parte|Integración por parte]] para integrar productos de funciones. |
| − | * Integración de | + | * [[Integración de Funciones_trigonométricas|funciones trigonométricas]]. |
| − | * Integración de funciones racionales.. | + | * [[Integración de funciones racionales|Integración de funciones racionales]]. |
| + | |||
| + | == Aplicaciones == | ||
| + | |||
| + | Con una integral puedes calcular magnitudes tan diversas como [[Área|áreas]], [[Cuerpos_geométricos_(Volumen)|volúmenes]], [http://es.wikipedia.org/wiki/Longitud_de_arco longitudes de curvas], el [http://es.wikipedia.org/wiki/Trabajo_%28f%C3%ADsica%29 trabajo] realizado por una fuerza, la [[Masa|masa de un sólido]], [http://es.wikipedia.org/wiki/Momento_de_inercia momentos de inercia],el [http://es.wikipedia.org/wiki/Campo_el%C3%A9ctrico campo eléctrico], el flujo de un fluido a través de una superficie y muchas más. Es notable, sin embargo, que la forma de proceder sea casi siempre la misma, y consiste en expresar el valor exacto de la magnitud que se quiere calcular como un [[Límite_de_una_función|límite]] de sumas de [[Bernhard_Riemann|Riemann]], para deducir, a partir de ellas, la integral cuyo cálculo proporciona la solución del problema. | ||
== Vea también == | == Vea también == | ||
| Línea 99: | Línea 106: | ||
* [[Integral Definida|Integral Definida]] | * [[Integral Definida|Integral Definida]] | ||
| + | |||
| + | * [[Integración_por_el_método_cambio_de_variable|Integración por Cambio de variable]] | ||
| + | |||
| + | * [[Integración por parte|Integración por parte]] | ||
| + | |||
| + | * [[Integración de Funciones_trigonométricas|funciones trigonométricas]]. | ||
| + | |||
| + | * [[Integración de funciones racionales|Integración de funciones racionales]]. | ||
* [[Derivada_de_una_función|Derivada de una función]] | * [[Derivada_de_una_función|Derivada de una función]] | ||
| Línea 107: | Línea 122: | ||
* Integrales inmediatas [citado 2011 agosto, 8]; Disponible en:http://es.wikipedia.org/wiki/Integraci%C3%B3n_indefinida | * Integrales inmediatas [citado 2011 agosto, 8]; Disponible en:http://es.wikipedia.org/wiki/Integraci%C3%B3n_indefinida | ||
| − | |||
[[Category:Matemáticas]] | [[Category:Matemáticas]] | ||
última versión al 21:44 12 ago 2019
| ||||||
Integral indefinida. Es el conjunto de las infinitas primitivas que puede tener una función.
Sumario
Definición
Integrar es el proceso recíproco del de derivar, es decir, dada una función f(x), busca aquellas funciones F(x) que al ser derivadas conducen a f(x).
Se dice, entonces, que F(x) es una primitiva o antiderivada de f(x); dicho de otro modo las primitivas de f(x) son las funciones derivables F(x) tales que:
F'(x) = f(x).
Si una función f(x) tiene primitiva, tiene infinitas primitivas, diferenciándose todas ellas en una constante.
[F(x) + C]' = F'(x) + 0 = F'(x) = f(x)
Integral indefinida
Integral indefinida es el conjunto de las infinitas primitivas que puede tener una función.
Se representa por ∫ f(x) dx.
Se lee como "la integral indefinida de f(x) respecto a x" Por lo tanto, f(x) dx es una conjunto de funciones; no es una función sola, ni un número.
La función f que se está integrando se llama el integrando, y la variable x se llama la variable de integración.
C es la constante de integración y puede tomar cualquier valor numérico real.
Si F(x) es una primitiva de f(x) se tiene que:
∫ f(x) dx = F(x) + C
Para comprobar que la primitiva de una función es correcta basta con derivar.
Integrales inmediatas
Si u = x (u' = 1), tenemos una tabla de integrales simples:
- ∫ cos x dx = sen x + C
Propiedades
1. La integral del producto de una constante por una función es igual a la constante por la integral de la función.
∫ k f(x) dx = k ∫f(x) dx
2. La integral de una suma de funciones es igual a la suma de las integrales de esas funciones.
∫[f(x) + g(x)] dx =∫ f(x) dx +∫ g(x) dx
Ejemplos
Métodos de integración
Se entiende por métodos de integración cualquiera de las diferentes técnicas elementales usadas para calcular una antiderivada o integral indefinida de una función.
Así, dada una función f(x), los métodos de integración son técnicas cuyo uso (usualmente combinado) permite encontrar una función F(x) tal que
F(x)=∫ ƒ(x) dx
lo cual, por el teorema fundamental del cálculo equivale a hallar una función F(x) tal que f(x) es su derivada.
Existen varios métodos entre los que se destacan los siguientes:
- Integración por Cambio de variable.
- Integración por parte para integrar productos de funciones.
- funciones trigonométricas.
- Integración de funciones racionales.
Aplicaciones
Con una integral puedes calcular magnitudes tan diversas como áreas, volúmenes, longitudes de curvas, el trabajo realizado por una fuerza, la masa de un sólido, momentos de inercia,el campo eléctrico, el flujo de un fluido a través de una superficie y muchas más. Es notable, sin embargo, que la forma de proceder sea casi siempre la misma, y consiste en expresar el valor exacto de la magnitud que se quiere calcular como un límite de sumas de Riemann, para deducir, a partir de ellas, la integral cuyo cálculo proporciona la solución del problema.
Vea también
Fuentes
- Integral indefinida [citado 2011 agosto, 8]; Disponible en:http://www.vitutor.com/integrales/indefinidas/integral_indefinida.html
- Integrales inmediatas [citado 2011 agosto, 8]; Disponible en:http://es.wikipedia.org/wiki/Integraci%C3%B3n_indefinida