Diferencia entre revisiones de «Pirámide»
| Línea 1: | Línea 1: | ||
{{Desarrollo}} {{Definición|Nombre=Pirámide|imagen=pirámide_plantilla.JPG|concepto=Sólido que tiene por base un [[Polígono|polígono]] cualquiera y cuyas caras, tantas en número como los lados de aquel, son [[Triángulo|triángulos]] que se juntan en un solo punto, llamado vértice.}}'''Pirámide (Figura). '''Es un [[Poliedro|poliedro]] limitado por una base, que es un polígono cualquiera, y varias caras laterales, que son [[Triángulo|triángulos]] con un vértice común llamado vértice de la pirámide. | {{Desarrollo}} {{Definición|Nombre=Pirámide|imagen=pirámide_plantilla.JPG|concepto=Sólido que tiene por base un [[Polígono|polígono]] cualquiera y cuyas caras, tantas en número como los lados de aquel, son [[Triángulo|triángulos]] que se juntan en un solo punto, llamado vértice.}}'''Pirámide (Figura). '''Es un [[Poliedro|poliedro]] limitado por una base, que es un polígono cualquiera, y varias caras laterales, que son [[Triángulo|triángulos]] con un vértice común llamado vértice de la pirámide. | ||
<div align="justify"> | <div align="justify"> | ||
| − | == Elementos<br> == | + | == Elementos<br> == |
| − | *'''Altura''': Es el segmento perpendicular a la base, que une la base con el vértice. | + | *'''Altura''': Es el segmento perpendicular a la base, que une la base con el vértice. |
*'''Vértices''': Son los puntos en donde se encuentran cada par de aristas.<br> | *'''Vértices''': Son los puntos en donde se encuentran cada par de aristas.<br> | ||
| − | *'''Aristas''': Son los lados de la base o de las caras latarales. Las aristas de la base se llaman aristas básicas y las aristas que concurren en el vértice, superior aristas laterales. [[Image: | + | *'''Aristas''': Son los lados de la base o de las caras latarales. Las aristas de la base se llaman aristas básicas y las aristas que concurren en el vértice, superior aristas laterales. [[Image:Pirámide elementos.JPG|thumb|right]] |
*'''Base''': Se llama base, al [[Polígono|polígono]] que delimita a la pirámide, y cuyos vértices no coinciden con en el vértice de la pirámide. '''Cara lateral''': Cada uno de los [[Triángulo|triángulos]] laterales que delimitan a la pirámide, y que al menos un vértice coincide con el de la pirámide. | *'''Base''': Se llama base, al [[Polígono|polígono]] que delimita a la pirámide, y cuyos vértices no coinciden con en el vértice de la pirámide. '''Cara lateral''': Cada uno de los [[Triángulo|triángulos]] laterales que delimitan a la pirámide, y que al menos un vértice coincide con el de la pirámide. | ||
| Línea 90: | Línea 90: | ||
== Volumen == | == Volumen == | ||
| − | [[Image:Pirámide volumen.JPG|thumb|right]]Supongamos que tenemos una pirámide de altura (h) y que la superficie (área) de su base tiene un valor A<sub>b</sub>.<br>El volumen (V)de la pirámide vendría dado por la fórmula: [[Image:Pirámide forvolumen.JPG|71x32px|Pirámide forvolumen.JPG]]<br>Donde V, A<sub>b, </sub>y h deben ir expresadas en unidades de medida que se correspondan; por ejemplo, si h se expresa en cm, A<sub>b</sub> irá en cm<sup>2</sup> y V en cm<sup>3</sup>. | + | [[Image:Pirámide volumen.JPG|thumb|right|Pirámide volumen.JPG]]Supongamos que tenemos una pirámide de altura (h) y que la superficie (área) de su base tiene un valor A<sub>b</sub>.<br>El volumen (V)de la pirámide vendría dado por la fórmula: [[Image:Pirámide forvolumen.JPG|71x32px|Pirámide forvolumen.JPG]]<br>Donde V, A<sub>b, </sub>y h deben ir expresadas en unidades de medida que se correspondan; por ejemplo, si h se expresa en cm, A<sub>b</sub> irá en cm<sup>2</sup> y V en cm<sup>3</sup>. |
'''Nota''': el volumen de una pirámide es una tercera parte del volumen de un prisma recto que tenga la misma base y la misma altura. | '''Nota''': el volumen de una pirámide es una tercera parte del volumen de un prisma recto que tenga la misma base y la misma altura. | ||
| − | [[Image:Pirámide y prisma recto.JPG|thumb|center|207x71px]]<br> | + | [[Image:Pirámide y prisma recto.JPG|thumb|center|207x71px|Pirámide y prisma recto.JPG]]<br> |
| + | |||
| + | == Pirámide Regular == | ||
| + | |||
| + | Una pirámide es regular si su base es un polígono regular y el vértice se proyecta (cae perpendicularmente) sobre el centro de la base. En una pirámide regular las caras laterales son triángulos isósceles cuyas alturas se llaman apotemas de la pirámide. <br><br> | ||
== Véase también == | == Véase también == | ||
Revisión del 14:53 13 mar 2011
| ||||||
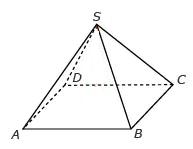
Pirámide (Figura). Es un poliedro limitado por una base, que es un polígono cualquiera, y varias caras laterales, que son triángulos con un vértice común llamado vértice de la pirámide.
Sumario
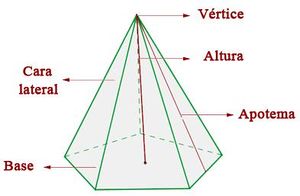
Elementos
- Altura: Es el segmento perpendicular a la base, que une la base con el vértice.
- Vértices: Son los puntos en donde se encuentran cada par de aristas.
- Aristas: Son los lados de la base o de las caras latarales. Las aristas de la base se llaman aristas básicas y las aristas que concurren en el vértice, superior aristas laterales.
- Base: Se llama base, al polígono que delimita a la pirámide, y cuyos vértices no coinciden con en el vértice de la pirámide. Cara lateral: Cada uno de los triángulos laterales que delimitan a la pirámide, y que al menos un vértice coincide con el de la pirámide.
- Apotema: Es la altura de cualquiera de sus caras laterales, o la distancia entre el centro de la base a cualquiera de sus lados.
Tipos
- Pirámide oblicua. Los vértices están marcados en naranja y las aristas en rojo. La línea amarilla es una diagonal de la base.
- Pirámide recta. Es un tipo de pirámide cuyas caras laterales son triángulos isósceles. En este tipo de pirámides la recta perpendicular a la base que pasa por el ápice corta a la base por su circuncentro.
- Pirámide oblicua. Es aquella en la que no todas sus caras laterales son triángulos isósceles.
- Pirámide regular. Es una pirámide recta cuya base es un polígono regular.
- Pirámide convexa. Tiene como base un polígono convexo.
- Pirámide cóncava. Tiene como base un polígono cóncavo.
Clasificación
|
Cant de lados |
Polígono de la base |
Clasificación de la Pirámide |
| 3 |
Triángulo |
Triangular(Tetraedro) |
| 4 |
Cuadrilátero |
Cuadrangular |
| 4 |
Rectángulo |
Rectangular |
| 5 |
Pentágono |
Pentagonal |
| 6 |
Hexágono |
Hexagonal |
| 7 |
Heptágono |
Heptagonal |
| 8 | Octágono | Octagonal |
| 9 |
Eneágono |
Eneagonal |
Área
Como cualquier poliedro, la pirámide posee área. En dependencia de lo que se quiere calcular podemos calcular su área de la base, área lateral, o el área total.
Área de la base
Como la base de la pirámide, puede ser cualquier polígono, entonces llamamos área de la base(Ab) de la pirámide, al área del polígono que conforma su base, independientemente de su clasificación, por ejemplo, la base de la pirámide puede ser un triángulo, un cuadrilátero, etc.
Área lateral
Las caras laterales de la pirámide son triángulos, y habrá tantas caras laterales como lados tenga el polígono de la base. Entonces el área lateral de la pirámide(AL) se calcula como la suma de todas las áreas de los triángulos que conforman las caras laterales. AL =A1 + A2 + A3 + ……
Área total
El área total de la pirámide (AT) se calcula como la suma de su área de la base(Ab) y el área lateral (AL), es decir, con la fórmula: AT = Ab + AL
Volumen
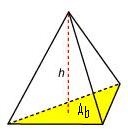
Supongamos que tenemos una pirámide de altura (h) y que la superficie (área) de su base tiene un valor Ab.El volumen (V)de la pirámide vendría dado por la fórmula:
Donde V, Ab, y h deben ir expresadas en unidades de medida que se correspondan; por ejemplo, si h se expresa en cm, Ab irá en cm2 y V en cm3.
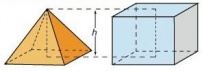
Nota: el volumen de una pirámide es una tercera parte del volumen de un prisma recto que tenga la misma base y la misma altura.
Pirámide Regular
Una pirámide es regular si su base es un polígono regular y el vértice se proyecta (cae perpendicularmente) sobre el centro de la base. En una pirámide regular las caras laterales son triángulos isósceles cuyas alturas se llaman apotemas de la pirámide.
Véase también
Fuentes