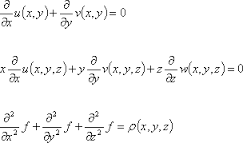Ecuación diferencial ordinaria
(Redirigido desde «Cálculo Diferencial»)
| ||||||
Ecuación diferencial ordinaria . Se asume que un cuerpo cuya temperatura es T0 en el instante de tiempo t = 0, se halla en un ambiente cuya temperatura es a ( T0 > a). Se requiere hallar la ley según la cual varía la temperatura del cuerpo, en función del tiempo. De la física se sabe que la velocidad de enfriamiento del cuerpo es proporcional a la diferencia de temperatura y la del medio ambiente.
Considerando que la función T(t) es decreciente y usando para el caso la derivada de la temperatura respecto al tiempo, se obtiene
- T´(t) = -k[T(t) - a] (1) donde k es el coeficiente de proporcionalidad.
- La ecuación (1) es el modelo matemático del proceso planteado. Se llama ecuación diferencial, pues junto con la función incógnita T(t) involucra además su derivada.
- La solución de la ecuación (1) es T(t) = C e-kt +a. Donde C es una constante arbitraria. El valor de esta constante puede ser obtenida de la condición T(0) = T0, esto es que la temperatura del cuerpo en el instante t= 0 es T0. Resultando T0 = C +a.
- Por último la solución buscada es T(t) = (T0- a) e -kt + a.Ya. s.[1]
Nomenclatura
- Como la función T= T(t) es de una sola variable, la ecuación se denomina ecuación diferencial ordinaria, (EDO).
- Puesto que que sólo hay derivada de primer orden esta ecuación se denomina EDO de primer orden.
- El valor C se conoce como constante arbitraria, resultado de la integral indefinida, que comporta una familia de funciones.
- La solución que conlleva la constante arbitraria C, se llama solución general.
- En el caso de que se conozcan los valores iniciales del tiempo t y de la temperatura T, se obtiene una solución particular, a partir de la solución general.
Referencia
- ↑ Bugrov; S.M. Nikolski. Matemáticas superiores Ecuaciones diferenciales Integrales múltiples Series Funciones de Variable compleja. Editorial Mir, Moscú -1985
Bibliografía
- Dennis G. Zill. Ecuaciones diferenciales con aplicaciones.