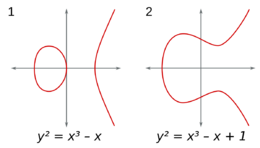
Curva elíptica

Curvas elípticas.
Información sobre la plantilla
Curva.png
Concepto:La Criptografía de Curva Elíptica (del inglés: Elliptic curve cryptography, ECC) es una variante de la criptografía asimétrica o de clave pública basada en las matemáticas de las curvas elípticas.

Curva Elíptica (del inglés: Elliptic curve cryptography, ECC) es una variante de la criptografía asimétrica o de clave pública basada en las matemáticas de las curvas elípticas.

Definición

Las curvas elípticas pueden definirse sobre cualquier cuerpo K; la definición formal de una curva elíptica es la de una curva algebraica proyectiva no singular sobre K de género 1. Si la característica K no es ni 2 ni 3, entonces toda curva elíptica sobre K puede escribirse en la forma: donde p y q son elementos de K tales que el polinomio del miembro derecho no tenga ninguna raíz doble. Si la característica es 2 o 3 harán falta más términos. Normalmente se define la curva como el conjunto de todos los puntos (x,y) que satisfacen la ecuación anterior, y tales que x e y sean elementos de la cerradura algebraica de K. Los puntos de la curva cuyas coordenadas pertenezcan ambas a K se llaman puntos K-racionales.

Ley de grupo en una curva elíptica

Una curva elíptica sobre un cuerpo K\mathbb K es una curva algebraica sin puntos singulares que viene dada por una ecuación del tipo y2+a1xy+a3y=x3+a2x2+a4x+a6,ai∈K,y^2 + a_1xy + a_3y = x^3 + a_2x^2 + a_4x + a_6 , \qquad a_i \in \mathbb K ,denominada ecuación general de Weierstrass.

Si la característica del cuerpo es distinta de 22 y de 33, usando transformaciones lineales de las variables, la ecuación de la curva se puede expresar como y2=x3+ax+b,a,b∈K,(1)\begin{equation} \label{ERW} y^2 = x^3 + ax + b , \qquad a , b \in \mathbb K , \end{equation} denominada ecuación reducida de Weierstrass, debiendo ser el discriminante del polinomio cúbico en xx no nulo, es decir, 4⋅a3+27⋅b2≠04 \cdot a^3 + 27 \cdot b^2 \neq 0, para que la curva no tenga singularidades.

Criptografía de curva elíptica

En general, los sistemas de criptografía de clave pública están basados en problemas matemáticos de muy difícil resolución. El sistema RSA, que ya examinamos en el Boletín ENIGMA nº 46, debía su fortaleza al hecho de que factorizar números grandes es una tarea computacionalmente compleja, tanto más cuanto mayor sea el número utilizado. En el sistema RA, sin embargo, las claves han de ser mucho más grandes que en el caso de los algoritmos simétricos para otorgar una seguridad parecida. Se conoce desde hace tiempo un tipo de criptografía de clave pública que requiere claves más pequeñas. Conocida bajo el nombre de Criptografía de Curva Elíptica (ECC), ha sido apenas usada hasta ahora, pero el hecho de que requiere claves más pequeñas que otros sistemas de clave pública lo hacen un buen candidato para aplicaciones donde los requisitos de tamaño de memoria son más exigentes, como por ejemplo en sistemas de identificación mediante tarjetas.

Como contrapartida, son sistemas más engorrosos de entender desde el punto de vista matemático. Pero para eso estamos aquí. Vamos a intentar descifrar el funcionamiento de los sistemas ECC. Les advierto que va a ser algo pesado, pero como de costumbre pondré las neuronas a funcionar con el objeto de simplificar en lo posible la explicación. El lector juzgará hasta qué punto he tenido éxito. Vamos a comenzar a cocinar. Para este plato necesitaremos logaritmos, grupos, puntos y operaciones. Si en el caso del algoritmo RSA, el problema consistía en factorizar números, en la ECC se trata de obtener logaritmos. Por si alguien no tiene fresco el concepto, recordemos. Supongamos que tenemos una expresión del tipo a^x=b, donde el signo ^ quiere decir “elevado a”. Para “despejar” x, utilizamos la operación inversa a la potenciación, y eso es el logaritmo. Esto es, si a^x=b, entonces x=Log(a)b, lo que se lee “x es el logaritmo en base a de b” Si a=10, hablamos de logaritmos decimales, y si a es el número e (=2.71828…), tenemos logaritmos naturales o neperianos. Bueno, en principio hallar un logaritmo no comporta mayor problema que hallar una potencia. Así que vamos a complicar las cosas en seguida. En primer lugar, necesitaremos un grupo. No se trata de una agrupación de personas. En álgebra, un grupo es un conjunto de elementos unidos a una operación matemática. Dicha operación matemática (llamémosla *) debe cumplir las siguientes propiedades:

  • Si a,b son elementos del grupo, su combinación a*b también es
  • un elemento del grupo
  • La operación cumple la propiedad asociativa: a*(b*c)=(a*b)*c
  • Existe el elemento neutro 1, tal que 1*a=a*1 para cualquier a
  • Existe el elemento opuesto, y, tal que x*y=y*x=1.

Por ejemplo, el conjunto de números enteros con la operación suma (y el cero como elemento neutro) formaría un grupo. Existen muchos tipos de grupos. Los que nos interesan se denominan “grupos cíclicos”. Un grupo cíclico se caracteriza porque todos sus elementos se pueden obtener mediante un sólo elemento, llamado generador. Si la operación es la multiplicación, se denomina grupo cíclico multiplicativo. Como ejemplo, podemos tomar el grupo formado por las cuatro raíces cuartas de 1: +1,-1,+i,-i (i es la raíz cuadrada de uno). El número i puede servir de multiplicador. En efecto:

i*(+1) = i i*(+i) = -1 i*(-1) = -i i*(-i) = 1 El concepto de grupo multiplicativo nos permite complicar la obtención de logaritmos. Supongamos un grupo G con n elementos, y sea b un generador. Eso significa que podemos obtener todos los elementos del grupo como {1, b, b^2, b^3 … b^(n-1)}. Es decir, habrá un número entero k de forma que podamos escribir g=b^k para cualquier número g del grupo. En realidad, existen muchos números enteros k que cumplan esta propiedad. Por ejemplo, el número k’=k+n también nos vale, puesto que b^(k+n)=(b^k)*(b^n),y b^n=1. Esto nos dice que cualesquiera dos enteros k,k´ capaces de representar el elemento g son congruentes módulo n (o dicho de otra forma: nos dan el mismo resto al dividirlos por n). Me huelo la cara que estará poniendo. Así que, antes de que pierda usted el apetito, vamos a aderezar el guiso con el elemento filipino: los logaritmos discretos. ¿Recuerda? Bien, se trataba de que si a^x=b, entonces x=Log(a)b. Aquí tenemos algo muy similar. La diferencia es que, en lugar de movernos por todo el campo de los números reales, nos restringiremos al grupo cíclico G. El LOGARITMO DISCRETO de g en base b es la operación inversa a la potenciación: si g=b^k, entonces k=Log(b)g.

En el caso de nuestro grupo, tendríamos b=i, k=0,1,2,3: b^k=g k=Log(b)g. i*1 = i 1 = Log(i)i i*2 = -1 2 = Log(i)(-1) i*3 = -i 3 = Log(i)(-i) i*4 = 1 4 = Log(i)(1) Vale, ya está. La salsa está lista. Ahora, la pregunta del millón es ¿y esto qué complicación tiene? Nos hemos aburrido como locos con todo ese rollo de los grupos multiplicativos, total, para terminar haciendo un logaritmo. El problema está cuando el grupo es muy grande. En nuestro caso, el número n es pequeño, de forma que he podido generar los elementos g como b^k (k=1,2,3,4). Si quiero saber cuál es el logaritmo discreto de -i no tengo más que mirar en la tabla y leer “i^3=-i”, de forma que la respuesta que busco es k=3. Pero, ¿y si el número n es muy grande? ¿Y si es enorme? ¿Y si n es 2^100? !Ah! Entonces tengo un problema gordo. !A ver quién se dedica a calcular g, g^2, g^3 … hasta g^(2^100)! Calcularlos todos requiere un tiempo de ejecución polinómico, lo que nos deja en la cuneta cuando n alcanza valores grandes. Es decir, podemos hacer operaciones del tipo g=b^k fácilmente, pero su inversa k=Log(b) ya es mucho más difícil. Nos recuerda el caso del algoritmo RSA: es fácil multiplicar dos números primos grandes, pero resulta mucho más difícil factorizar el producto. ¿Y dónde entran las curvas elípticas? Básicamente, y simplificando mucho, nos permiten crear el grupo G. Según sea el grupo, así de complicado será el problema y, por tanto, así de seguro será el esquema a efectos de montar sistemas de cifrado. Por ejemplo, el algoritmo de cifrado Diffle-Hellman (bueno, en realidad es de intercambio de claves, pero viene a ser lo mismo) usa un grupo que se denota como Zn* y que se lee “”grupo multiplicativo de enteros módulo n”. No es necesario aquí saber qué significa, así que sean buenos y no me obliguen a explicárselo. Volvamos a las curvas elípticas. ¿Recuerdan sus tiempos de instituto?. La ecuación y=ax+b nos daba una recta, x^2+y^2=r^2 representaba una circunferencia … y la curva del tipo y^2=x^3+ax+b nos da nuestra curva elíptica. Para cada pareja de valores (a,b), la curva nos da un montón de puntos (x,y). Añadiremos el “punto en el infinito” a efectos de complitud. Ese montón de puntos forma un grupo. Es importante distinguir entre dos conceptos: los números x,y son reales y forman un campo finito (otro bicho matemático como el grupo, pero con propiedades distintas), pero los puntos (x,y) forman un grupo. Es como una coordenada en un plano. Si decimos “longitud 4.3, latiud 45.8″, los números 4.3 y 45.8 son una cosa, pero el lugar geográfico que representan es otra. Por eso suele hablarse de “grupos multiplicativos de campos finitos”. Puede parecer complicado, pero por lo que parece el problema de logaritmos discretos en los grupos generados mediante curvas elípticas es más complejo que el correspondiente al grupo de elementos muitlplicativos no nulos subyacentes al campo en sí (y si no lo han entendido, lo tachan y ya está).

El esquema sería algo así: a) Escogemos una curva elíptica b) La curva elíptica tiene un conjunto de soluciones (x,y). c) Si los valores x,y pertenecen a un campo finito, entonces los puntos (x,y) de la curva forman un grupo d) Tomamos un elemento del grupo, y hallamos su logaritmo discreto para una base dada. Eso nos servirá de base para establecer algoritmos criptográficos de intercambio de claves y de firma digital. Mis disculpas por lo engorroso del tema, y coincido con ustedes en que quienes inventaron todo ese galimatías debería ser puesto en busca y captura. Los “sospechosos habituales” son Victor Millery Neil Koblitz, quienes descubrieron la ECC en 1985 como mecanismo alternativo para distribución de claves. En cualquier caso, el hecho es que la ECC es mucho más compleja que el sistema RSA, tiene más incertidumbres y puede que nos de más de una sorpresa. También es bastante lento, al menos en su implementacióninicial. En el apartado positivo, requiere claves de longitud menor que las RSA, aunque todavía mayores que las de los algoritmos simétricos. Según el NIST (el instituto de estándares de EEUU), el algoritmo simétrico AES con clave de 128 bits proporciona una seguridad aproximadamente igual a la de ECC con clave de 256 bits … o a la del algoritmo asimétrico RSA con clave de 3072 bits. Quizá el mayor inconveniente del esquema ECC sea legal: según la NSA norteamericana, la empresa Certicom tiene más de 130 patentes en ese campo, lo que seguramente desanima a más de uno. Claro que la propia NSA tiene un acuerdo de licencia con Certicom, y acepta dos algoritmos basados en ECC dentro de su “Suite B” de algoritmos de cifrado y firma. Así que algo debe tener.

Curva elíptica ECDSA.

Elliptic Curve Digital Signature Algorithm es una modificación del algoritmo DSA que emplea operaciones sobre puntos de curvas elípticas en lugar de las exponenciaciones que usa DSA (problema del logaritmo discreto). La principal ventaja de este esquema es que requiere números de tamaños menores para brindar la misma seguridad que DSA o RSA. Existen dos tipos de curvas dependiendo del campo finito en el que se definan, que pueden ser GF(P) o GF(2m).

Factorización de curva elíptica de Lenstra

La factorización de curva elíptica de Lenstra o método de factorización de curva elíptica ( del inglés elliptic curve factorization method, ECM) es un rápido algoritmo de tiempo de ejecución sub-exponencial para la factorización de enteros que emplea curvas elípticas. Para una factorización de propósito general, ECM es el tercer método más rápido conocido de factorización. El segundo más rápido es la criba cuadrática de múltiples polinomios y el más rápido es la criba general del cuerpo de números. La factorización de curva elíptica de Lenstra es llamada así en honor a Hendrik Lenstra. En la práctica, ECM es considerado un algoritmo de factorización de propósito especial así como el más adecuado para encontrar factores pequeños. A fecha de 2012, es todavía el mejor algoritmo para divisores que no superen los 20 a 25 dígitos decimales (64 a 83 bits respectivamente), así como su tiempo de ejecución está dominado por el tamaño del factor más pequeño p en lugar de por el tamaño del número n a ser factorizado. Frecuentemente, ECM se usa para eliminar factores pequeños de un entero muy grande con muchos factores; si el entero resultante todavía es compuesto, entonces solo tiene factores grandes y es factorizado mediante el uso de técnicas de propósito general. El factor más grande encontrado usando ECM cuenta con 75 dígitos y fue descubierto el 2 de agosto de 2012 por Samuel Wagstaff.1 Incrementando el número de curvas probadas se mejoran las posibilidades de encontrar un factor, pero no son lineales con el incremento en el número de dígitos.

Fuentes

Obtenido de «https://www.ecured.cu/index.php?title=Curva_elíptica&oldid=3268735»