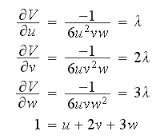Diferencia entre revisiones de «Método de Lagrange»
(Etiqueta: nuestro-nuestra) |
|||
| (No se muestran 7 ediciones intermedias de 3 usuarios) | |||
| Línea 1: | Línea 1: | ||
| − | |||
| − | |||
{{Definición | {{Definición | ||
|nombre= Método de Lagrange | |nombre= Método de Lagrange | ||
| − | |imagen= | + | |imagen=MétododeLagrange.jpg |
|tamaño= | |tamaño= | ||
| − | |concepto= Método para trabajar con funciones de varias variables que nos interesa maximizar o minimizar, y está sujeta a ciertas restricciones.}} | + | |concepto= Método para trabajar con funciones de varias variables que nos interesa maximizar o minimizar, y está sujeta a ciertas restricciones.}}'''Método de Lagrange'''. Este método reduce el problema restringido en ''n'' variables en uno sin restricciones de ''n + 1'' variables cuyas ecuaciones pueden ser resueltas. |
| − | + | ||
| − | '''Método de Lagrange''' Este método reduce el problema restringido en n variables en uno sin restricciones de n + 1 variables cuyas ecuaciones pueden ser resueltas | + | == Generalidades == |
| − | + | En los problemas de optimización, los multiplicadores de Lagrange, nombrados así en honor a [[Joseph Louis Lagrange]], son un método para trabajar con funciones de varias variables que nos interesa maximizar o minimizar, y está sujeta a ciertas restricciones. Este método reduce el problema restringido en '''''n''''' variables en uno sin restricciones de '''n + 1''' variables cuyas ecuaciones pueden ser resueltas. | |
| − | En los problemas de optimización, los multiplicadores de Lagrange, nombrados así en honor a Joseph Louis Lagrange, son un método para trabajar con funciones de varias variables que nos interesa maximizar o minimizar, y está sujeta a ciertas restricciones. Este método reduce el problema restringido en n variables en uno sin restricciones de n + 1 variables cuyas ecuaciones pueden ser resueltas. | + | |
| + | Este método introduce una nueva variable escalar desconocida, el multiplicador de Lagrange, para cada restricción y forma una combinación lineal involucrando los multiplicadores como coeficientes. Su demostración involucra derivadas parciales, o bien usando diferenciales totales, o sus parientes cercanos, la regla de la cadena. El fin es, usando alguna función implícita, encontrar las condiciones para que la derivada con respecto a las variables independientes de una [[función]] sea igual a cero. | ||
| − | |||
==Péndulo simple == | ==Péndulo simple == | ||
| − | + | Se denimina péndulo simple a un ente ideal constituido por una [[masa]] puntual suspendido de un hilo inextensible y sin [[peso]], capaz de oscilar libremente en el vacío y sin rozamiento. Al separar la masa de su posición de [[equilibrio]], oscila a ambos lados de dicha posición, realizando un movimiento armónico simple. Naturalmente es imposible la realización práctica de un péndulo simple, pero si es accesible a la teoría. | |
El péndulo simple o matemático se denomina así en contraposición a los péndulos reales, compuestos o físicos, únicos que pueden construirse. | El péndulo simple o matemático se denomina así en contraposición a los péndulos reales, compuestos o físicos, únicos que pueden construirse. | ||
| − | |||
| − | |||
==Método Newton== | ==Método Newton== | ||
| − | + | Al considerarse un péndulo simple, si se desplaza la [[partícula]] desde la posición de [[equilibrio]] hasta que el hilo forme un ángulo Θ con la vertical, y luego se abandona partiendo del reposo, el péndulo oscilará en un plano vertical bajo la acción de la gravedad. | |
| − | + | Las oscilaciones tendrán lugar entre las posiciones extremas Θ y -Θ, simétricas respecto a la vertical, a lo largo de un arco de circunferencia cuyo radio es la longitud, \ell, del hilo. El movimiento es periódico, pero no se puede asegurar que sea armónico. | |
| − | [[ | + | Para determinar la naturaleza de las oscilaciones se debe de escribir la [[ecuación]] del movimiento de la partícula. La partícula se mueve sobre un arco de [[circunferencia]] bajo la acción de dos fuerzas: su propio [[peso]] (mg) y la tensión del hilo (N). |
| − | |||
| − | |||
| − | [[ | ||
| − | |||
| − | [[ | ||
| − | |||
==Polinomios de Lagrange == | ==Polinomios de Lagrange == | ||
| − | Suponiendo que se conoce por lo menos [[ | + | Suponiendo que se conoce por lo menos |
| − | + | ||
| − | [[Archivo:For2. | + | [[Archivo:For1.JPG]] |
| − | para [[ | + | |
| − | [[ | + | se propone: |
| + | |||
| + | [[Archivo:For2.JPG]] | ||
| + | |||
| + | para [[Archivo:For3.JPG]] | ||
| + | [[Archivo:For4.JPG]] | ||
| + | |||
por lo tanto: [[Archivo:For5.JPG]] | por lo tanto: [[Archivo:For5.JPG]] | ||
| + | |||
para [[Archivo:For6.JPG]] | para [[Archivo:For6.JPG]] | ||
| + | |||
[[Archivo:For7.JPG]] | [[Archivo:For7.JPG]] | ||
[[Archivo:For8.JPG]] | [[Archivo:For8.JPG]] | ||
| − | |||
| − | *Para la Solución de Problemas de Optimización Dinámica: La resolución de un problema de interpolación lleva a un problema de [[álgebra lineal]] en el cual se debe resolver un sistema de ecuaciones. Usando una | + | ==Ayudas que brinda == |
| + | |||
| + | * Para la '''''Solución de Problemas de Optimización Dinámica''''': La resolución de un problema de interpolación lleva a un problema de [[álgebra lineal]] en el cual se debe resolver un sistema de ecuaciones. Usando una base monómica estándar para el [[polinomio]] interpolador, se llega a la matriz de Vandermonde. Eligiendo una base distinta, la base de Lagrange, se llega a la forma más simple de matriz identidad = δi que puede resolverse inmediatamente. | ||
| − | *Multiplicadores de Langrange: Llamados así en honor a [[Joseph Louis Lagrange]], es un procedimiento para encontrar los máximos y mínimos de funciones de varias variables sujetas a restricciones | + | * '''''Multiplicadores de Langrange''''': Llamados así en honor a [[Joseph Louis Lagrange]], es un procedimiento para encontrar los máximos y mínimos de funciones de varias variables sujetas a restricciones |
==Véase también== | ==Véase también== | ||
| − | * Joseph Louis Lagrange | + | * [[Joseph Louis Lagrange]]. |
| − | |||
| − | |||
| − | |||
==Fuente== | ==Fuente== | ||
| − | * Artículo [http://www.wikimatematica.org/index.php?title=M%C3%A9todo_de_Lagrange Método de Lagrange] | + | * Artículo. [http://www.wikimatematica.org/index.php?title=M%C3%A9todo_de_Lagrange Método de Lagrange] Disponible en: "www.wikimatematica.org". Consultado: 9 de septiembre de 2011. |
| − | *Artículo [http://www.cccp.org.co/index.php/component/content/article/167 Instrumentación oceanográfica]. Disponible en "www.cccp.org.co". Consultado: 10 de septiembre | + | * Artículo. [http://www.cccp.org.co/index.php/component/content/article/167 Instrumentación oceanográfica]. Disponible en: "www.cccp.org.co". Consultado: 10 de septiembre de 2011. |
| − | * | + | * Artículo. [http://www.webpondo.org/fhamann/lagrange_slides.pdf Método de Lagrange para la Solución de Problemas de - WEBPONDO]. Disponible en: "www.webpondo.org". Consultado 10 de septiembre de 2011. |
| − | |||
| − | |||
| − | [[Category:Instrumentos_de_medición]] | + | [[Category:Matemáticas]][[Category:Física]][[Category:Instrumentos_de_medición]] |
última versión al 08:40 16 jul 2013
| ||||||
Método de Lagrange. Este método reduce el problema restringido en n variables en uno sin restricciones de n + 1 variables cuyas ecuaciones pueden ser resueltas.
Sumario
Generalidades
En los problemas de optimización, los multiplicadores de Lagrange, nombrados así en honor a Joseph Louis Lagrange, son un método para trabajar con funciones de varias variables que nos interesa maximizar o minimizar, y está sujeta a ciertas restricciones. Este método reduce el problema restringido en n variables en uno sin restricciones de n + 1 variables cuyas ecuaciones pueden ser resueltas.
Este método introduce una nueva variable escalar desconocida, el multiplicador de Lagrange, para cada restricción y forma una combinación lineal involucrando los multiplicadores como coeficientes. Su demostración involucra derivadas parciales, o bien usando diferenciales totales, o sus parientes cercanos, la regla de la cadena. El fin es, usando alguna función implícita, encontrar las condiciones para que la derivada con respecto a las variables independientes de una función sea igual a cero.
Péndulo simple
Se denimina péndulo simple a un ente ideal constituido por una masa puntual suspendido de un hilo inextensible y sin peso, capaz de oscilar libremente en el vacío y sin rozamiento. Al separar la masa de su posición de equilibrio, oscila a ambos lados de dicha posición, realizando un movimiento armónico simple. Naturalmente es imposible la realización práctica de un péndulo simple, pero si es accesible a la teoría.
El péndulo simple o matemático se denomina así en contraposición a los péndulos reales, compuestos o físicos, únicos que pueden construirse.
Método Newton
Al considerarse un péndulo simple, si se desplaza la partícula desde la posición de equilibrio hasta que el hilo forme un ángulo Θ con la vertical, y luego se abandona partiendo del reposo, el péndulo oscilará en un plano vertical bajo la acción de la gravedad.
Las oscilaciones tendrán lugar entre las posiciones extremas Θ y -Θ, simétricas respecto a la vertical, a lo largo de un arco de circunferencia cuyo radio es la longitud, \ell, del hilo. El movimiento es periódico, pero no se puede asegurar que sea armónico.
Para determinar la naturaleza de las oscilaciones se debe de escribir la ecuación del movimiento de la partícula. La partícula se mueve sobre un arco de circunferencia bajo la acción de dos fuerzas: su propio peso (mg) y la tensión del hilo (N).
Polinomios de Lagrange
Suponiendo que se conoce por lo menos
se propone:
Ayudas que brinda
- Para la Solución de Problemas de Optimización Dinámica: La resolución de un problema de interpolación lleva a un problema de álgebra lineal en el cual se debe resolver un sistema de ecuaciones. Usando una base monómica estándar para el polinomio interpolador, se llega a la matriz de Vandermonde. Eligiendo una base distinta, la base de Lagrange, se llega a la forma más simple de matriz identidad = δi que puede resolverse inmediatamente.
- Multiplicadores de Langrange: Llamados así en honor a Joseph Louis Lagrange, es un procedimiento para encontrar los máximos y mínimos de funciones de varias variables sujetas a restricciones
Véase también
Fuente
- Artículo. Método de Lagrange Disponible en: "www.wikimatematica.org". Consultado: 9 de septiembre de 2011.
- Artículo. Instrumentación oceanográfica. Disponible en: "www.cccp.org.co". Consultado: 10 de septiembre de 2011.
- Artículo. Método de Lagrange para la Solución de Problemas de - WEBPONDO. Disponible en: "www.webpondo.org". Consultado 10 de septiembre de 2011.