Diferencia entre revisiones de «Clúster no jerárquico»
(→Algoritmo CLARA) |
|||
| (No se muestran 6 ediciones intermedias del mismo usuario) | |||
| Línea 1: | Línea 1: | ||
{{Materia | {{Materia | ||
| − | |nombre=Clúster no | + | |nombre=Clúster no jerárquico |
| − | |imagen= | + | |imagen=PAM12.jpeg |
|campo a que pertenece= | |campo a que pertenece= | ||
|principales exponentes= | |principales exponentes= | ||
}} | }} | ||
| − | '''Los procedimientos de aglomeración no jerarquizados''' tambiénse llaman métodos de aglomeración de K-medias. En los rocedimientos no jerárquicos no se construyen árboles. En su lugar, se asignan los objetos a conglomerados una vez que el número de conglomerados a formar está especificado. | + | '''Los procedimientos de aglomeración no jerarquizados''' tambiénse llaman métodos de aglomeración de K-medias. En los rocedimientos no jerárquicos no se construyen [[árboles]]. En su lugar, se asignan los objetos a [[conglomerados]] una vez que el número de conglomerados a formar está especificado. |
| − | + | ==Funciones en software R.== | |
| − | En el leguaje R (R Development Core Team2016) se implementan una serie de algoritmos no jerárquicos. En el paquete stats se puede encontrar la función kmeans() del método de aglomeración de K-medias y en el paquete | + | En el leguaje R (R Development Core Team2016) se implementan una serie de algoritmos no jerárquicos. En el paquete stats se puede encontrar la función kmeans() del método de aglomeración de K-medias y en el paquete [[clúster]] las funciones pam(), clara() y fanny() para los métodos pam, clara y fanny respectivamente. |
Ejemplos para los cuatros métodos en códigos de R:<br /> | Ejemplos para los cuatros métodos en códigos de R:<br /> | ||
| Línea 18: | Línea 18: | ||
iris.scaled<- scale(iris[, -5])<br /> | iris.scaled<- scale(iris[, -5])<br /> | ||
| − | + | ==Agrupamiento K-means== | |
| − | R dispone de la función kmeans() con 4 métodos de agrupamiento.<br /> | + | R dispone de la [[función]] kmeans() con 4 métodos de agrupamiento.<br /> |
set.seed(123)<br /> | set.seed(123)<br /> | ||
km.HW<- kmeans(iris.scaled, 3, algorithm = "Hartigan-Wong", nstart = 25)<br /> | km.HW<- kmeans(iris.scaled, 3, algorithm = "Hartigan-Wong", nstart = 25)<br /> | ||
| Línea 34: | Línea 34: | ||
plot(iris.scaled, col =km.HW$cluster)# Visualización de los conglomerados<br /> | plot(iris.scaled, col =km.HW$cluster)# Visualización de los conglomerados<br /> | ||
points(km.HW$centers, col = 1:2, pch = 8, cex = 2)<br /> | points(km.HW$centers, col = 1:2, pch = 8, cex = 2)<br /> | ||
| − | + | [[Archivo:Kmedias12.jpeg|left|miniaturadeimagen]] | |
| − | + | <br /> | |
| − | (PartitioningAroundMedoids), usa k- | + | <br /> |
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | ==Algoritmo PAM== | ||
| + | (PartitioningAroundMedoids), usa k-medoid para identificar agrupamientos,trabaja bien en bases de datos pequeñas, pero es lento en grandes. Un medoidese podría definir como el objeto perteneciente a un cluster o conglomerado, cuyo promedio de disimilaridad a todos los objetos en el conglomerado es mínima, es decir, que se puede considerar como el punto máscéntrico de la agrupación considerada.<br /> | ||
Agrupamiento PAM<br /> | Agrupamiento PAM<br /> | ||
| Línea 42: | Línea 50: | ||
summary(pam.res)<br /> | summary(pam.res)<br /> | ||
plot(pam.res)<br /> | plot(pam.res)<br /> | ||
| − | + | [[Archivo:PAM12.jpeg|left|miniaturadeimagen]] | |
| − | + | <br /> | |
| − | (ClusteringLargeApplications) crea múltiples muestras de | + | <br /> |
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | ==Algoritmo CLARA== | ||
| + | (ClusteringLargeApplications) crea múltiples muestras de los datos y después aplica PAM a la muestra.<br /> | ||
Agrupamiento CLARA<br /> | Agrupamiento CLARA<br /> | ||
| − | + | clara.I<- clara(iris.scaled, 2)<br /> | |
| − | + | clara.I<br /> | |
| − | + | clara.I$clusinfo<br /> | |
| − | plot( | + | plot(clara.I,ask = TRUE)<br /> |
| − | + | [[Archivo:Clara12.jpeg|left|miniaturadeimagen]] | |
| − | + | <br /> | |
| − | utiliza un valor “k” que indica el número de grupos a formar 0 < k < n/2; n es el número de observaciones.Es un análisis de conglomerados donde cada individuo tiene un grado de pertenencia difuso a los grupos. | + | <br /> |
| − | + | <br /> | |
| − | + | <br /> | |
| − | summary( | + | <br /> |
| − | plot( | + | <br /> |
| − | + | <br /> | |
| − | Para su ejecución se requiere de una plataforma Windows® y el lenguaje de programación, orientado a objetos, denominado R. Este es un lenguaje de programación y un entorno para el análisis estadístico y la realización de gráficos. | + | <br /> |
| + | ==Algoritmo FANNY== | ||
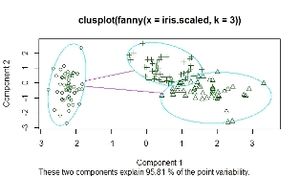
| + | utiliza un valor “k” que indica el número de grupos a formar 0 < k < n/2; n es el número de observaciones.Es un análisis de conglomerados donde cada individuo tiene un grado de pertenencia difuso a los grupos.<br /> | ||
| + | Agrupamiento FANNY<br /> | ||
| + | fanny.I<- fanny(iris.scaled, 3)<br /> | ||
| + | summary(fanny.I)<br /> | ||
| + | plot(fanny.I, ask = TRUE)<br /> | ||
| + | [[Archivo:Fanny12.jpeg|left|miniaturadeimagen]] | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | ==Requerimientos== | ||
| + | Para su ejecución se requiere de una plataforma [[Windows®]] y el lenguaje de programación, orientado a objetos, denominado R. Este es un lenguaje de programación y un entorno para el análisis estadístico y la realización de gráficos. | ||
==Fuentes== | ==Fuentes== | ||
última versión al 13:24 6 abr 2017
| ||||
Los procedimientos de aglomeración no jerarquizados tambiénse llaman métodos de aglomeración de K-medias. En los rocedimientos no jerárquicos no se construyen árboles. En su lugar, se asignan los objetos a conglomerados una vez que el número de conglomerados a formar está especificado.
Sumario
Funciones en software R.
En el leguaje R (R Development Core Team2016) se implementan una serie de algoritmos no jerárquicos. En el paquete stats se puede encontrar la función kmeans() del método de aglomeración de K-medias y en el paquete clúster las funciones pam(), clara() y fanny() para los métodos pam, clara y fanny respectivamente.
Ejemplos para los cuatros métodos en códigos de R:
Cargar base de datos
data(iris)
head(iris)
remover la columna cinco y escalar los datos
iris.scaled<- scale(iris[, -5])
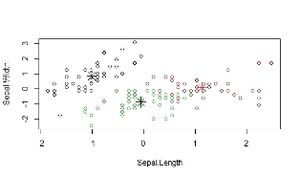
Agrupamiento K-means
R dispone de la función kmeans() con 4 métodos de agrupamiento.
set.seed(123)
km.HW<- kmeans(iris.scaled, 3, algorithm = "Hartigan-Wong", nstart = 25)
km.L<- kmeans(iris.scaled, 3, algorithm = "Lloyd", nstart = 25)
km.F<- kmeans(iris.scaled, 3, algorithm = "Forgy", nstart = 25)
km.MQ<- kmeans(iris.scaled, 3, algorithm = "MacQueen", nstart = 25)
km.HW$cluster# número de conglomerado de pertenencia de cada individuo
km.HW$centers#Centros de los grupos (media de los individuos en cada variable)
km.HW$withinss#Suma de cuadrados dentro de grupos.
km.HW$size#Número de individuos asignados a cada grupo
km.HW$totss#Suma total de los cuadrados
km.HW$tot.withinss#Suma de cuadrados de los 3 grupos
km.HW$betweenss#La resta de la suma de cuadrados total menos la suma de #cuadrados de los 3 grupos (totss - tot.withinss)
plot(iris.scaled, col =km.HW$cluster)# Visualización de los conglomerados
points(km.HW$centers, col = 1:2, pch = 8, cex = 2)
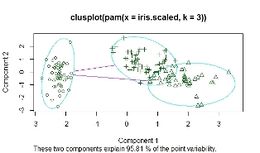
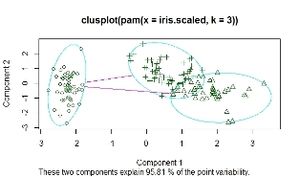
Algoritmo PAM
(PartitioningAroundMedoids), usa k-medoid para identificar agrupamientos,trabaja bien en bases de datos pequeñas, pero es lento en grandes. Un medoidese podría definir como el objeto perteneciente a un cluster o conglomerado, cuyo promedio de disimilaridad a todos los objetos en el conglomerado es mínima, es decir, que se puede considerar como el punto máscéntrico de la agrupación considerada.
Agrupamiento PAM
pam.I<- pam(iris.scaled, 3)
summary(pam.res)
plot(pam.res)
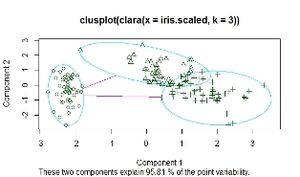
Algoritmo CLARA
(ClusteringLargeApplications) crea múltiples muestras de los datos y después aplica PAM a la muestra.
Agrupamiento CLARA
clara.I<- clara(iris.scaled, 2)
clara.I
clara.I$clusinfo
plot(clara.I,ask = TRUE)
Algoritmo FANNY
utiliza un valor “k” que indica el número de grupos a formar 0 < k < n/2; n es el número de observaciones.Es un análisis de conglomerados donde cada individuo tiene un grado de pertenencia difuso a los grupos.
Agrupamiento FANNY
fanny.I<- fanny(iris.scaled, 3)
summary(fanny.I)
plot(fanny.I, ask = TRUE)
Requerimientos
Para su ejecución se requiere de una plataforma Windows® y el lenguaje de programación, orientado a objetos, denominado R. Este es un lenguaje de programación y un entorno para el análisis estadístico y la realización de gráficos.
Fuentes
- Leiva-Valdebenito, Susana A., & Torres-Avilés, Francisco J.. (2010). Una revisión de los algoritmos de partición más comunes en el análisis de conglomerados: un estudio comparativo. Revista Colombiana de Estadística, 33(2), 321-339. Disponible en: www.scielo.org.co/pdf/rce/v33n2/v33n2a09.pdf
- Johnson DE (2000) Métodos Multivariados aplicados al análisis de datos. In: International Thomson Editores SA (ed)
- R Development Core Team. 2016. R: A language and environment for statistical computing. R Foundation for Statistical Computing. R Foundation for Statistical Computing. (consultado: 22 septiembre 2016, http://www.r-project.org/)