Diferencia entre revisiones de «Numeración decimal»
(Página creada con '{{Definición|Nombre=Numeración decimal|imagen= Numeración decimal.jpg|concepto=Sistema de símbolos creado por los romanos}}'''Numeración decimal'''. Los números nos sirven...') (Etiqueta: nuestro-nuestra) |
(Etiqueta: nuestro-nuestra) |
||
| Línea 1: | Línea 1: | ||
| − | {{Definición|Nombre=Numeración decimal|imagen= Numeración decimal.jpg|concepto=Sistema de | + | {{Definición|Nombre=Numeración decimal|imagen= Numeración decimal.jpg|concepto=Sistema de numeración utilizado en [[Cuba]]}}'''Numeración decimal'''. Los números nos sirven para contar seres, objetos, etc., es decir, cualquier cantidad de todo lo que nos rodea. Para poder escribir cualquier número, hemos de usar caracteres o símbolos, que hemos de combinar según unas reglas que forman lo que llamamos un sistema de numeración. En [[Cuba]] se utiliza el sistema de numeración decimal. |
| − | == El sistema de numeración decimal== | + | == El sistema de numeración decimal == |
| − | |||
| − | |||
| − | |||
| − | [[ | + | A lo largo de la historia ha habido distintos sistemas de numeración, como el maya, el chino o el [[Números_Romanos|sistema Romano]], con símbolos y reglas diferentes a los nuestros. Nuestro sistema de numeración (el decimal) procede de la [[India|India]], aunque fueron los árabes los que lo introdujeron en [[Europa|Europa]]. Este sistema numérico está definido por la base que utiliza (base 10). La base es el número de símbolos diferentes, o guarismos necesarios para representar un número cualquiera, de los infinitos posibles, en el sistema. El sistema de numeración decimal necesita diez símbolos diferentes o dígitos para representar un número. |
| − | + | [[Image:Digitos.jpg|thumb|center|211x50px|Dígitos de la Numeración decimal]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Multiplicando por 10 a los dígitos se forman las decenas. Con las decenas y las unidades se forman los números de dos cifras. <br> | |
| − | |||
| − | |||
| − | |||
| − | + | Multiplicando por 100 a los dígitos se forman las centenas. Con las centenas, las decenas y las unidades se forman los números de tres cifras. <br> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | 2- Leemos los grupos empezando por el primero de la izquierda: | + | Los números de 4 a 6 cifras además de las unidades, decenas y centenas tienen las unidades, decenas y centenas de millar. <br> |
| − | • “cuarenta y tres | + | |
| − | En los | + | Los números de 7 a 12 cifras tienen, además, las unidades, decenas, centenas,…, de millón. <br> |
| − | En los | + | |
| − | Téngase presente que debe suprimirse el mil si las 3 cifras que le preceden son ceros. Igualmente se suprimen las palabras millón, billón, trillón, etc, si son ceros las 6 cifras anteriores a sus números indicadores. | + | Los de más de 12 cifras tienen, además, unidades, decenas, centenas,…, de billón, trillón, etc. tienen las unidades, decenas y centenas de millar.<br> |
| + | |||
| + | Se llama sistema decimal o de base 10, porque 10 unidades de un orden cualquiera forman 1 unidad del orden inmediato superior<br> | ||
| + | |||
| + | Es un sistema posicional porque el valor de una cifra depende de la posición que ocupe dentro del número que estemos considerando. | ||
| + | |||
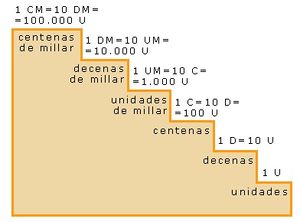
| + | [[Image:Escala1decimal.JPG|thumb|right|Escala hasta la centena de millar]]Los seis primeros órdenes de unidades son: <br> | ||
| + | |||
| + | *Centenas de Millar (CM) | ||
| + | *Decenas de Millar (DM) | ||
| + | *Unidades de Millar (UM) | ||
| + | *Centenas (C) | ||
| + | *Decenas (D) | ||
| + | *Unidades (U)<br><br> | ||
| + | |||
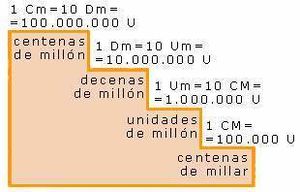
| + | [[Image:Escala2decimal.jpg|thumb|right|Escala hasta las centenas de millón]]Para números más grandes con más de seis cifras, hemos de usar órdenes de unidades superiores a la centena de millar: <br> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | == Cómo escribir un número == | ||
| + | |||
| + | A lo largo de la historia ha habido distintos sistemas de numeración, como el maya, el chino o el sistema Romano, con símbolos y reglas diferentes a los nuestros. Nuestro sistema de numeración (el decimal) procede de la India, aunque fueron los árabes los que lo introdujeron en Europa. Este sistema numérico está definido por la base que utiliza (base 10). La base es el número de símbolos diferentes, o guarismos necesarios para representar un número cualquiera, de los infinitos posibles, en el sistema. El sistema de numeración decimal necesita diez símbolos diferentes o dígitos para representar un número. | ||
| + | |||
| + | == Cómo leer un número == | ||
| + | |||
| + | Para leer cualquier número hemos de formar grupos de tres cifras, contándolas desde la derecha y recorriendo el número hacia la izquierda, dejando los espacios vacíos indicadores de los millares, millones, billones, etc, en su lugar correspondiente Después se lee cada uno de los grupos, empezando por el primero de la izquierda y avanzando hacia la derecha. Ejemplo: Leer el número: 43 526 625 213 032 004 080 068 1- Formamos grupos de tres cifras: | ||
| + | |||
| + | 2- Leemos los grupos empezando por el primero de la izquierda: • “cuarenta y tres mil quinientos veintiséis trillones, seiscientos veinticinco mil doscientos trece billones, treinta y dos mil cuatro millones, ochenta mil sesenta y ocho”. En los espacio vacío impares (primer, tercer, quinto, etc) de derecha a izquierda se dice mil En los espacio vacío pares (segundo, cuarto, sexto, etc) de derecha a izquierda se dice millón, billón, trillón, etc Téngase presente que debe suprimirse el mil si las 3 cifras que le preceden son ceros. Igualmente se suprimen las palabras millón, billón, trillón, etc, si son ceros las 6 cifras anteriores a sus números indicadores. | ||
== Comparar un número == | == Comparar un número == | ||
| − | 1. Contar el número de cifras de los números y es mayor el que más cifras tenga. | + | |
| − | 2. Si tienen el mismo número de cifras será mayor el que tenga mayor la primera cifra comenzando por la izquierda. Si las primeras cifras son iguales se analizan las siguientes y así sucesivamente. | + | 1. Contar el número de cifras de los números y es mayor el que más cifras tenga. 2. Si tienen el mismo número de cifras será mayor el que tenga mayor la primera cifra comenzando por la izquierda. Si las primeras cifras son iguales se analizan las siguientes y así sucesivamente. Ejemplo: a) 22 384 584 > 6 360 624 porque el primero tiene más cifras que el segundo. b) 34 345 < 2 456 678 porque el segundo tiene más cifras que el primero c) 3 284 321 > 2 181 382 Porque 3 > 2. d) 3 181 382 < 3 284 321 pues 3 = 3 y 1 < 2 e) 4 321 108 > 4 321 105 pues 8 > 5 y las cifras anteriores son iguales. |
| − | Ejemplo: | + | |
| − | a) 22 384 584 | ||
| − | b) 34 345 | ||
| − | c) 3 284 321 | ||
| − | d) 3 181 382 | ||
| − | e) 4 321 108 | ||
== Fuentes == | == Fuentes == | ||
| Línea 46: | Línea 57: | ||
*[[Sócrates Rosell|Rosell Franco, Sócrates]]. Aritmética, Volumen I, Editora Pedagógica. [[La Habana|La Habana]], [[1966|1966]]. | *[[Sócrates Rosell|Rosell Franco, Sócrates]]. Aritmética, Volumen I, Editora Pedagógica. [[La Habana|La Habana]], [[1966|1966]]. | ||
| + | [[Category:Teoría_elemental_de_los_números]] | ||
| − | + | <br> | |
Revisión del 09:56 8 dic 2010
| ||||||
Numeración decimal. Los números nos sirven para contar seres, objetos, etc., es decir, cualquier cantidad de todo lo que nos rodea. Para poder escribir cualquier número, hemos de usar caracteres o símbolos, que hemos de combinar según unas reglas que forman lo que llamamos un sistema de numeración. En Cuba se utiliza el sistema de numeración decimal.
Sumario
El sistema de numeración decimal
A lo largo de la historia ha habido distintos sistemas de numeración, como el maya, el chino o el sistema Romano, con símbolos y reglas diferentes a los nuestros. Nuestro sistema de numeración (el decimal) procede de la India, aunque fueron los árabes los que lo introdujeron en Europa. Este sistema numérico está definido por la base que utiliza (base 10). La base es el número de símbolos diferentes, o guarismos necesarios para representar un número cualquiera, de los infinitos posibles, en el sistema. El sistema de numeración decimal necesita diez símbolos diferentes o dígitos para representar un número.
Multiplicando por 10 a los dígitos se forman las decenas. Con las decenas y las unidades se forman los números de dos cifras.
Multiplicando por 100 a los dígitos se forman las centenas. Con las centenas, las decenas y las unidades se forman los números de tres cifras.
Los números de 4 a 6 cifras además de las unidades, decenas y centenas tienen las unidades, decenas y centenas de millar.
Los números de 7 a 12 cifras tienen, además, las unidades, decenas, centenas,…, de millón.
Los de más de 12 cifras tienen, además, unidades, decenas, centenas,…, de billón, trillón, etc. tienen las unidades, decenas y centenas de millar.
Se llama sistema decimal o de base 10, porque 10 unidades de un orden cualquiera forman 1 unidad del orden inmediato superior
Es un sistema posicional porque el valor de una cifra depende de la posición que ocupe dentro del número que estemos considerando.
Los seis primeros órdenes de unidades son:
- Centenas de Millar (CM)
- Decenas de Millar (DM)
- Unidades de Millar (UM)
- Centenas (C)
- Decenas (D)
- Unidades (U)
Para números más grandes con más de seis cifras, hemos de usar órdenes de unidades superiores a la centena de millar:
Cómo escribir un número
A lo largo de la historia ha habido distintos sistemas de numeración, como el maya, el chino o el sistema Romano, con símbolos y reglas diferentes a los nuestros. Nuestro sistema de numeración (el decimal) procede de la India, aunque fueron los árabes los que lo introdujeron en Europa. Este sistema numérico está definido por la base que utiliza (base 10). La base es el número de símbolos diferentes, o guarismos necesarios para representar un número cualquiera, de los infinitos posibles, en el sistema. El sistema de numeración decimal necesita diez símbolos diferentes o dígitos para representar un número.
Cómo leer un número
Para leer cualquier número hemos de formar grupos de tres cifras, contándolas desde la derecha y recorriendo el número hacia la izquierda, dejando los espacios vacíos indicadores de los millares, millones, billones, etc, en su lugar correspondiente Después se lee cada uno de los grupos, empezando por el primero de la izquierda y avanzando hacia la derecha. Ejemplo: Leer el número: 43 526 625 213 032 004 080 068 1- Formamos grupos de tres cifras:
2- Leemos los grupos empezando por el primero de la izquierda: • “cuarenta y tres mil quinientos veintiséis trillones, seiscientos veinticinco mil doscientos trece billones, treinta y dos mil cuatro millones, ochenta mil sesenta y ocho”. En los espacio vacío impares (primer, tercer, quinto, etc) de derecha a izquierda se dice mil En los espacio vacío pares (segundo, cuarto, sexto, etc) de derecha a izquierda se dice millón, billón, trillón, etc Téngase presente que debe suprimirse el mil si las 3 cifras que le preceden son ceros. Igualmente se suprimen las palabras millón, billón, trillón, etc, si son ceros las 6 cifras anteriores a sus números indicadores.
Comparar un número
1. Contar el número de cifras de los números y es mayor el que más cifras tenga. 2. Si tienen el mismo número de cifras será mayor el que tenga mayor la primera cifra comenzando por la izquierda. Si las primeras cifras son iguales se analizan las siguientes y así sucesivamente. Ejemplo: a) 22 384 584 > 6 360 624 porque el primero tiene más cifras que el segundo. b) 34 345 < 2 456 678 porque el segundo tiene más cifras que el primero c) 3 284 321 > 2 181 382 Porque 3 > 2. d) 3 181 382 < 3 284 321 pues 3 = 3 y 1 < 2 e) 4 321 108 > 4 321 105 pues 8 > 5 y las cifras anteriores son iguales.
Fuentes
- Microsoft ® Encarta ® 2007. © 1993--2006. Microsoft Corporation. Reservados todos los derechos.
- Rosell Franco, Sócrates. Aritmética, Volumen I, Editora Pedagógica. La Habana, 1966.