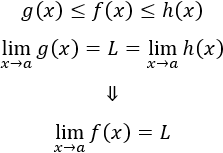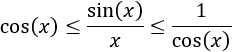Diferencia entre revisiones de «Teorema del emparedado»
(Nuevo artículo) |
m |
||
| Línea 1: | Línea 1: | ||
| − | El '''teorema del emparedado''' (llamado también '''teorema del sándwich''', '''teorema de encaje''', '''teorema del bocadillo''' y '''teorema de comparación''', entre otros) es | + | El '''teorema del emparedado''' (llamado también '''teorema del sándwich''', '''teorema de encaje''', '''teorema del bocadillo''' y '''teorema de comparación''', entre otros) es un resultado que permite calcular el [[límite de una función]] por comparación con otras dos funciones. |
== Teorema == | == Teorema == | ||
| Línea 16: | Línea 16: | ||
==Referencias== | ==Referencias== | ||
| − | [[Categoría: Límites]][[Categoría: matemáticas]] | + | [[Categoría: Límites]] |
| + | [[Categoría: matemáticas]] | ||
última versión al 04:19 8 jun 2019
El teorema del emparedado (llamado también teorema del sándwich, teorema de encaje, teorema del bocadillo y teorema de comparación, entre otros) es un resultado que permite calcular el límite de una función por comparación con otras dos funciones.
Sumario
Teorema
Sea I un intervalo que contiene al punto a y sean f, g y h funciones definidas en I, exceptuando quizás el mismo punto a. Si para todo x en I y diferente de a se cumple g(x) ≤ f(x) ≤ h(x) y, además, el límite de g(x) y el de h(x) cuando x tiende a a es L, entonces el límite de f(x) cuando x tiende a a también es L.
Ejemplo
El límite de la función sin(x)/x cuando x tiende a 0 es igual a 1. Para probarlo, se utiliza que, en un entorno de x=0,
Fuentes
- Criterio del emparedado, Matesfacil, ISSN: 2659-8442. Consultado el 8 de junio de 2019.