Diferencia entre revisiones de «Homotecia»
m (Texto reemplazado: «<div align="justify">» por «») |
|||
| (No se muestran 4 ediciones intermedias de otro usuario) | |||
| Línea 1: | Línea 1: | ||
| − | + | ||
{{Definición | {{Definición | ||
|nombre=Homotecia | |nombre=Homotecia | ||
| Línea 6: | Línea 6: | ||
|concepto=Una homotecia es una transformación afín que, a partir de un punto fijo, multiplica todas las distancias por un mismo [[factor]]. En general una homotecia de razón diferente de 1 deja un único punto fijo, llamado centro de la transformación. | |concepto=Una homotecia es una transformación afín que, a partir de un punto fijo, multiplica todas las distancias por un mismo [[factor]]. En general una homotecia de razón diferente de 1 deja un único punto fijo, llamado centro de la transformación. | ||
}} | }} | ||
| − | + | ||
| − | '''Homotecia'''. El estudio de la igualdad de figuras geométricas se hizo estrechamente relacionado con el concepto movimiento y si se aplica a una figura geométrica un movimiento se obtiene otra figura que es igual a ella. | + | '''Homotecia'''. El estudio de la igualdad de [[Figura geométrica|figuras geométricas]] se hizo estrechamente relacionado con el concepto movimiento y si se aplica a una figura geométrica un movimiento se obtiene otra figura que es igual a ella. |
== Determinación == | == Determinación == | ||
| Línea 20: | Línea 20: | ||
Una homotecia de centro O y razón k se denota H (O; k) | Una homotecia de centro O y razón k se denota H (O; k) | ||
| − | == Propiedades | + | == Propiedades == |
Para toda H(O; k) se cumple: 1. La imagen de una recta es una recta paralela a ella. 2. La imagen de un segmento es un segmento paralelo a el y que tiene k veces su longitud. 3. La imagen de un ángulo es un ángulo que tiene su misma amplitud. | Para toda H(O; k) se cumple: 1. La imagen de una recta es una recta paralela a ella. 2. La imagen de un segmento es un segmento paralelo a el y que tiene k veces su longitud. 3. La imagen de un ángulo es un ángulo que tiene su misma amplitud. | ||
| − | Las propiedades de la homotecia se pueden demostrar aplicando el teorema reciproco del Teorema de las transversales y el Teorema fundamental de la semejanza de triángulos. | + | Las propiedades de la homotecia se pueden demostrar aplicando el teorema reciproco del Teorema de las transversales y el Teorema fundamental de la semejanza de [[Triángulo|triángulos]]. |
| − | == Composición | + | == Composición == |
| − | === | + | === Movimiento === |
Cuando se realizan sucesivamente varios movimientos (por ejemplo si se hace una traslación a una figura, después se le aplica a la imagen obtenida una Simetría central y finalmente se le aplica a la nueva imagen, una reflexión) se obtiene una figura igual a la original. A esta realización sucesiva de movimientos se le denomina composición de movimientos. | Cuando se realizan sucesivamente varios movimientos (por ejemplo si se hace una traslación a una figura, después se le aplica a la imagen obtenida una Simetría central y finalmente se le aplica a la nueva imagen, una reflexión) se obtiene una figura igual a la original. A esta realización sucesiva de movimientos se le denomina composición de movimientos. | ||
| Línea 42: | Línea 42: | ||
===Figuras Semejantes=== | ===Figuras Semejantes=== | ||
| − | Toda composición de una homotecia con un [[Movimiento]] se llama transformación semejante. | + | Toda composición de una homotecia con un [[Movimiento|movimiento]] se llama transformación semejante. |
Todo movimiento es de hecho una transformación semejante, pues basta considerarlo como la composición de un movimiento con una homotecia de razón k = 1. Siempre se cumple que la imagen de una figura geométrica cualquiera por una transformación semejante, es semejante a la figura original. | Todo movimiento es de hecho una transformación semejante, pues basta considerarlo como la composición de un movimiento con una homotecia de razón k = 1. Siempre se cumple que la imagen de una figura geométrica cualquiera por una transformación semejante, es semejante a la figura original. | ||
| − | Dos figuras geométricas F1 y F2 son semejantes, si existe una transformación semejante por la cual una se trasforma en la otra. Se escribe entonces F1~ F2 | + | Dos figuras geométricas F1 y F2 son semejantes, si existe una transformación semejante por la cual una se trasforma en la otra. Se escribe entonces F1~ F2. |
== Véase también == | == Véase también == | ||
última versión al 21:27 12 ago 2019
| ||||||
Homotecia. El estudio de la igualdad de figuras geométricas se hizo estrechamente relacionado con el concepto movimiento y si se aplica a una figura geométrica un movimiento se obtiene otra figura que es igual a ella.
Sumario
Determinación
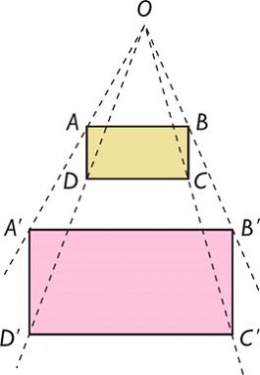
Una homotecia es una transformación del plano en si mismo que se define de la manera siguiente:
- Se determina un Punto O como centro de la homotecia.
- Se determina un número real como razón de la homotecia.
- La Imagen P' de un punto P está situada sobre la Semirrecta OP
- O es su propia imagen (O' y O coinciden).
Una homotecia de centro O y razón k se denota H (O; k)
Propiedades
Para toda H(O; k) se cumple: 1. La imagen de una recta es una recta paralela a ella. 2. La imagen de un segmento es un segmento paralelo a el y que tiene k veces su longitud. 3. La imagen de un ángulo es un ángulo que tiene su misma amplitud.
Las propiedades de la homotecia se pueden demostrar aplicando el teorema reciproco del Teorema de las transversales y el Teorema fundamental de la semejanza de triángulos.
Composición
Movimiento
Cuando se realizan sucesivamente varios movimientos (por ejemplo si se hace una traslación a una figura, después se le aplica a la imagen obtenida una Simetría central y finalmente se le aplica a la nueva imagen, una reflexión) se obtiene una figura igual a la original. A esta realización sucesiva de movimientos se le denomina composición de movimientos.
La composición de varios movimientos es también un movimiento. De forma análoga cuando sucesivamente se realizan varias homotecias, se habla entonces de composición de homotecias.
La composición de dos homotecias H (O1, k1) y H (O2, k2) donde k1• k2 =1 es nuevamente una homotecia, su razón k3 = k1 • k2 y su centro O3 se encuentra situado sobre la recta O1O2. También se puede hacer la composición de una homotecia con un movimiento.
Generalizando se puede definir una homotecia H (O; -k) con k > 0 como la composición de una homotecia H (O; k) con una simetría central de centro O.
Transformaciones Semejantes
Figuras Semejantes
Toda composición de una homotecia con un movimiento se llama transformación semejante.
Todo movimiento es de hecho una transformación semejante, pues basta considerarlo como la composición de un movimiento con una homotecia de razón k = 1. Siempre se cumple que la imagen de una figura geométrica cualquiera por una transformación semejante, es semejante a la figura original.
Dos figuras geométricas F1 y F2 son semejantes, si existe una transformación semejante por la cual una se trasforma en la otra. Se escribe entonces F1~ F2.
Véase también
Fuentes
- Libro de texto Matemática 9no grado, Editorial Pueblo y Educación, 2001
- [1]
- [2]
- [3]