Diferencia entre revisiones de «Grafo conexo»
(Página creada con '{{Definición|Nombre=Grafo conexo|imagen=K333.png|concepto=Grafo que entre cualquier par de sus vértices existe un camino que los un...') |
m (Texto reemplazado: «<div align="justify">» por «») |
||
| (No se muestran 4 ediciones intermedias de 2 usuarios) | |||
| Línea 1: | Línea 1: | ||
{{Definición|Nombre=Grafo conexo|imagen=K333.png|concepto=[[Grafo]] que entre cualquier par de sus [[Vértice (Grafo)|vértices]] existe un [[Camino (Grafo)|camino]] que los une.}} | {{Definición|Nombre=Grafo conexo|imagen=K333.png|concepto=[[Grafo]] que entre cualquier par de sus [[Vértice (Grafo)|vértices]] existe un [[Camino (Grafo)|camino]] que los une.}} | ||
| − | |||
| − | |||
| − | ==Definición | + | '''Grafo conexo'''. En matemáticas y ciencias de la computación es aquel [[grafo]] que entre cualquier par de sus vértices existe un Camino (Grafo) que los une. |
| + | |||
| + | ==Definición== | ||
Sea el grafo ''G=<V,A>'', donde ''V'' es el [[conjunto]] de los nodos o vértices y ''A'' es la colección de sus arcos o aristas en dependencia de si es un [[Dígrafo|grafo orientado]] o no orientado, se dice que ''G'' es '''conexo''' si y solo si entre cualquier par de vértices ''x'', ''y'' de ''V'' existe un camino que comience en ''x'' y termine en ''y''. | Sea el grafo ''G=<V,A>'', donde ''V'' es el [[conjunto]] de los nodos o vértices y ''A'' es la colección de sus arcos o aristas en dependencia de si es un [[Dígrafo|grafo orientado]] o no orientado, se dice que ''G'' es '''conexo''' si y solo si entre cualquier par de vértices ''x'', ''y'' de ''V'' existe un camino que comience en ''x'' y termine en ''y''. | ||
En el caso de los grafos no orientados [[Grafo simple|simples]] que entre cualquier par de vértices existe una arista que los une se hacen llamar [[Grafo completo|grafos completos]] y los que ''|V|=k'' se denominan [[Kn|K<sub>n</sub>]]. | En el caso de los grafos no orientados [[Grafo simple|simples]] que entre cualquier par de vértices existe una arista que los une se hacen llamar [[Grafo completo|grafos completos]] y los que ''|V|=k'' se denominan [[Kn|K<sub>n</sub>]]. | ||
| − | ==Conexidad en dígrafos | + | ==Conexidad en dígrafos== |
En los grafos dirigidos existen 3 tipos de niveles de conexidad por los que se llaman a los grafos como: | En los grafos dirigidos existen 3 tipos de niveles de conexidad por los que se llaman a los grafos como: | ||
| Línea 15: | Línea 15: | ||
* '''Fuertemente conexos''': Grafos orientados que entre cualquier par de nodos distintos existe un arco que los une. | * '''Fuertemente conexos''': Grafos orientados que entre cualquier par de nodos distintos existe un arco que los une. | ||
| + | Los grafos fuertemente conexos <u>nunca son simples</u> pues exige que siempre entre un par de vértices habrá un par de aristas (una de ida y otra de vuelta). | ||
| + | ==Ejemplos== | ||
| + | {| class="wikitable" | ||
| + | |- | ||
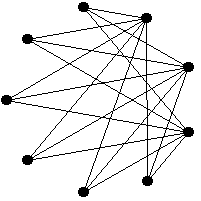
| + | | [[Image:K333.png|thumb|Grafo conexo]] | ||
| + | | [[Image:K5.png|thumb|Grafo completo]] | ||
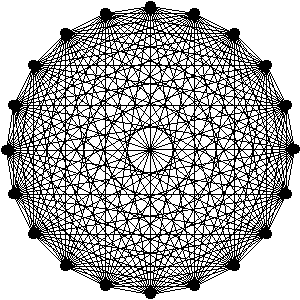
| + | | [[Image:K20.png|thumb|K<sub>20</sub>]] | ||
| + | |- | ||
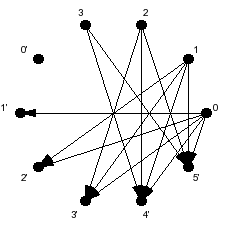
| + | | [[Image:Digrafo_asociado_ejemplo1.png|thumb|Dígrafo no conexo]] | ||
| + | | [[Image:Digrafo_asociado_ejemplo5.png|thumb|Dígrafo débil conexo]] | ||
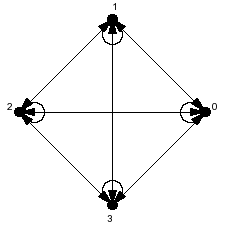
| + | | [[Image:Digrafo_asociado_ejemplo3.png|thumb|Fuerte conexo]] | ||
| + | |} | ||
| − | ==Veáse también | + | ==Veáse también== |
* [[Grafo]]. | * [[Grafo]]. | ||
| − | |||
* [[Teoría de grafos]]. | * [[Teoría de grafos]]. | ||
| − | ==Fuentes | + | ==Fuentes== |
| − | + | *K. Ribnikov. Análisis Combinatorio. Editorial Mir [[Moscú]]. [[1988]]. | |
| − | + | *Artículo [http://es.wikipedia.org/wiki/Grafo Grafo] Disponible en la Web "es.wikipedia.org" Consultado: 13 de septiembre de 2011. | |
| − | + | ||
[[Categoría:Álgebra]] | [[Categoría:Álgebra]] | ||
última versión al 01:37 22 ago 2019
| ||||||
Grafo conexo. En matemáticas y ciencias de la computación es aquel grafo que entre cualquier par de sus vértices existe un Camino (Grafo) que los une.
Definición
Sea el grafo G=<V,A>, donde V es el conjunto de los nodos o vértices y A es la colección de sus arcos o aristas en dependencia de si es un grafo orientado o no orientado, se dice que G es conexo si y solo si entre cualquier par de vértices x, y de V existe un camino que comience en x y termine en y.
En el caso de los grafos no orientados simples que entre cualquier par de vértices existe una arista que los une se hacen llamar grafos completos y los que |V|=k se denominan Kn.
Conexidad en dígrafos
En los grafos dirigidos existen 3 tipos de niveles de conexidad por los que se llaman a los grafos como:
- Conexos: Idéntico a la definición antes vista.
- Débilmente conexos: Dígrafos que no son conexos pero que sus equivalentes no orientados o sosías sí lo son.
- Fuertemente conexos: Grafos orientados que entre cualquier par de nodos distintos existe un arco que los une.
Los grafos fuertemente conexos nunca son simples pues exige que siempre entre un par de vértices habrá un par de aristas (una de ida y otra de vuelta).