Diferencia entre revisiones de «Función lineal»
(Página creada con '{{Definición |nombre= Función lineal |imagen= Funcion_lineal.JPG |tamaño= |concepto= La función que a cada x€R le hace corresponder un número real f(x) = mx + n. Donde m ...') (Etiqueta: no tiene enlaces internos) |
(Etiqueta: no tiene enlaces internos) |
||
| Línea 27: | Línea 27: | ||
[[Image:FL33.JPG]] | [[Image:FL33.JPG]] | ||
| + | |||
| + | Calculo de la pendiente de la recta | ||
| + | |||
| + | La pendiente m de la recta que pasa por los punto P1(x1; y1) y P2(x2; y2) se calcula por la fórmula | ||
| + | |||
| + | [[Image:Pendiente.JPG|border|Pendiente.JPG]] | ||
=== Cero de la función === | === Cero de la función === | ||
| Línea 33: | Línea 39: | ||
El elemento del dominio de la función lineal f(x) = mx + n (m ≠0) cuya imagen es cero, se denomina cero de esta función. | El elemento del dominio de la función lineal f(x) = mx + n (m ≠0) cuya imagen es cero, se denomina cero de esta función. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Véase también == | == Véase también == | ||
Revisión del 16:35 18 feb 2011
| ||||||
Función lineal: La función que a cada x€R le hace corresponder un número real f(x) = mx + n. Donde m y n son números reales dados, se denomina función lineal.
Características generales
Una función lineal según la primera definición dada anteriormente representa una aplicación lineal si y sólo si n = 0. Así, algunos autores llaman función lineal a aquella de la forma mientras que llaman función afín a la que tiene la forma
, cuando n es distinto de cero. La grafica de la función lineal es una recta.
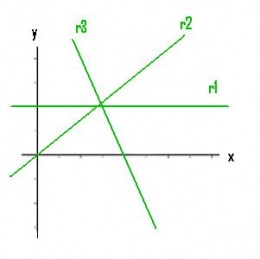
Los valores de m y n son constantes reales y x es una variable real. La constante m es la pendiente de la recta, y n es el punto de corte de la recta con el eje y. Cuando cambiamos m modificamos la inclinación de la recta y cuando cambiamos n desplazamos la línea arriba o abajo.
Pendiente
La pendiente es la inclinación de la recta con respecto al eje de abscisas.
Si m < 0, la recta se inclina hacia arriba, la función es creciente y el ángulo que forma la recta con la parte positiva del eje OX es agudo.
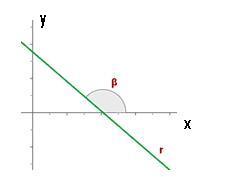
Si m > 0, la recta se inclina hacia abajo, la función es decreciente y el ángulo que forma la recta con la parte positiva del eje OX es obtuso.
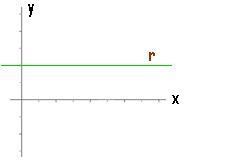
Si m = 0, la recta es paralela al eje x.
Calculo de la pendiente de la recta
La pendiente m de la recta que pasa por los punto P1(x1; y1) y P2(x2; y2) se calcula por la fórmula
Cero de la función
El dominio de la función lineal es el conjunto de los números reales.
El elemento del dominio de la función lineal f(x) = mx + n (m ≠0) cuya imagen es cero, se denomina cero de esta función.
Véase también
Fuente
- Baño Muñoz Felix. Colectivo de autores. Matemática 8vo grado.Editorial Pueblo y Educación. 1991.