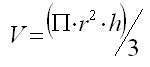Diferencia entre revisiones de «Cuerpos geométricos (Volumen)»
| Línea 3: | Línea 3: | ||
== Definición<br> == | == Definición<br> == | ||
| − | Proviene del vocablo[[ | + | Proviene del vocablo[[Latín|latín]] '''volūmen''', es la medida del espacio ocupado por un cuerpo. El volumen de los cuerpos es el resultado de sus tres dimensiones: ancho, alto y profundidad<br> |
== Cuerpos<br> == | == Cuerpos<br> == | ||
| Línea 9: | Línea 9: | ||
=== Cilindro<br> === | === Cilindro<br> === | ||
| − | Un cilindro es un cuerpo geométrico engendrado por un rectángulo que gira alrededor de uno de sus lados.[[Image:Cilindrof.gif|thumb|right | + | Un cilindro es un cuerpo geométrico engendrado por un rectángulo que gira alrededor de uno de sus lados.[[Image:Cilindrof.gif|thumb|right]]<br> |
Elementos de un cilindro:<br> | Elementos de un cilindro:<br> | ||
| Línea 19: | Línea 19: | ||
Volumen del cilindro:<br> | Volumen del cilindro:<br> | ||
| − | [[Image:Cilindro.jpg|thumb|left]] | + | [[Image:Cilindro.jpg|thumb|left|Cilindro.jpg]] |
<br> | <br> | ||
| Línea 29: | Línea 29: | ||
=== Esfera === | === Esfera === | ||
| − | Una esfera es un sólido cerrado delimitado por una superficie en la que todos los puntos se encuentran equidistantes[[Image:Esferaf.gif|thumb|right]] de un punto central llamado centro. <br> | + | Una esfera es un sólido cerrado delimitado por una superficie en la que todos los puntos se encuentran equidistantes[[Image:Esferaf.gif|thumb|right|Esferaf.gif]] de un punto central llamado centro. <br> |
Elementos de la esfera:<br> | Elementos de la esfera:<br> | ||
| Línea 37: | Línea 37: | ||
Volumen de la esfera: | Volumen de la esfera: | ||
| − | [[Image:Esfera.jpg|thumb|left]] | + | [[Image:Esfera.jpg|thumb|left|Esfera.jpg]] |
<br> | <br> | ||
| Línea 43: | Línea 43: | ||
<br> | <br> | ||
| − | + | <br> | |
=== Cono<br> === | === Cono<br> === | ||
| − | Es el cuerpo de revolución obtenido al hacer girar un triángulo rectángulo alrededor de uno de sus catetos.[[Image:Conof.gif|thumb|right]]<br> | + | Es el cuerpo de revolución obtenido al hacer girar un triángulo rectángulo alrededor de uno de sus catetos.[[Image:Conof.gif|thumb|right|Conof.gif]]<br> |
Elementos del cono<br> | Elementos del cono<br> | ||
| Línea 61: | Línea 61: | ||
Volumen del cono: | Volumen del cono: | ||
| − | [[Image:Cono.jpg|left]] | + | [[Image:Cono.jpg|left|Cono.jpg]] |
| + | <br> | ||
| + | |||
| + | <br> | ||
| − | |||
=== Prisma<br> === | === Prisma<br> === | ||
| − | Los prismas son poliedros que tienen dos caras paralelas e iguales llamadas bases y sus caras laterales son [[Image:Prismaf.gif|right|188x159px]]paralelogramos.<br> | + | Los prismas son poliedros que tienen dos caras paralelas e iguales llamadas bases y sus caras laterales son [[Image:Prismaf.gif|right|188x159px|Prismaf.gif]]paralelogramos.<br> |
Elementos de un prisma:<br> | Elementos de un prisma:<br> | ||
| Línea 77: | Línea 79: | ||
Los lados de las bases constituyen las aristas básicas y los lados de las caras laterales las aristas laterales, éstas son iguales y paralelas entre sí. <br> Volumen de un prisma: V= A<sub>B</sub> * h<br> | Los lados de las bases constituyen las aristas básicas y los lados de las caras laterales las aristas laterales, éstas son iguales y paralelas entre sí. <br> Volumen de un prisma: V= A<sub>B</sub> * h<br> | ||
| − | [[Image:Prisma.jpg|left]] | + | [[Image:Prisma.jpg|left|Prisma.jpg]] |
| + | |||
| + | |||
| + | |||
| + | |||
| Línea 83: | Línea 89: | ||
=== Pirámide<br> === | === Pirámide<br> === | ||
| − | Una pirámide es un poliedro, cuya base es un polígono cualquiera y cuyas caras laterales son triángulos con un vértice común, que es el vértice de la pirámide.<br> | + | Una pirámide es un poliedro, cuya base es un polígono cualquiera y cuyas caras laterales son triángulos con un vértice[[Image:Piramidef.gif|thumb|right]] común, que es el vértice de la pirámide.<br> |
Elementos de una pirámide<br> | Elementos de una pirámide<br> | ||
| Línea 93: | Línea 99: | ||
La apotema lateral de una pirámide regular es la altura de cualquiera de sus caras laterales.<br> | La apotema lateral de una pirámide regular es la altura de cualquiera de sus caras laterales.<br> | ||
| − | + | Volumen de la piramide:<br> | |
| + | |||
| + | [[Image:Piramide.jpg|left]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
== Poliedros regulares<br> == | == Poliedros regulares<br> == | ||
| Línea 99: | Línea 111: | ||
=== Tetraedro<br> === | === Tetraedro<br> === | ||
| − | Un tetraedro regular es un poliedro regular formado por 4 triángulos equiláteros iguales. Es una pirámide triangular regular.<br> | + | Un tetraedro regular es un poliedro regular formado por 4 triángulos equiláteros iguales. Es una pirámide triangular [[Image:Tetraedrof.gif|thumb|right]]regular.<br> |
Propiedades del tetraedro | Propiedades del tetraedro | ||
| Línea 112: | Línea 124: | ||
Volumen del tetraedro: <br> | Volumen del tetraedro: <br> | ||
| + | |||
| + | [[Image:Tetraedro.jpg|left]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
=== Octaedro === | === Octaedro === | ||
Revisión del 10:07 12 abr 2011
| ||||
Volumen: Es una magnitud escalar definida como el espacio ocupado por un cuerpo.
Sumario
Definición
Proviene del vocablolatín volūmen, es la medida del espacio ocupado por un cuerpo. El volumen de los cuerpos es el resultado de sus tres dimensiones: ancho, alto y profundidad
Cuerpos
Cilindro
Un cilindro es un cuerpo geométrico engendrado por un rectángulo que gira alrededor de uno de sus lados.
Elementos de un cilindro:
Eje: Es el lado fijo alrededor del cual gira el rectángulo.
Bases: Son los círculos que engendran los lados perpendiculares al eje.
Altura: Es la distancia entre las dos bases.
Generatriz: Es el lado opuesto al eje, y es el lado que engendra el cilindro.
La generatriz del cilindro es igual a la altura. h = g
Volumen del cilindro:
Esfera
Una esfera es un sólido cerrado delimitado por una superficie en la que todos los puntos se encuentran equidistantes
de un punto central llamado centro.
Elementos de la esfera:
Centro: Punto interior que equidista de cualquier punto de la superficie de la esfera.
Radio: Distancia del centro a un punto de la superficie de la esfera.
Cuerda: Segmento que une dos puntos de la superficie esférica.
Diámetro: Cuerda que pasa por el centro.
Polos: Son los puntos del eje de giro que quedan sobre la superficie esférica.
Volumen de la esfera:
Cono
Es el cuerpo de revolución obtenido al hacer girar un triángulo rectángulo alrededor de uno de sus catetos.
Elementos del cono
Eje: Es el cateto fijo alrededor del cual gira el triángulo.
Base: Es el círculo que forma el otro cateto.
Altura. Es la distancia del vértice a la base.
Generatriz: Es la hipotenusa del triángulo rectángulo.
Por el teorema de Pitágoras la generatriz del cono será igual a:
g2= h2 + r2
g=RAIZ Cuadrada(h2+r2)
Volumen del cono:
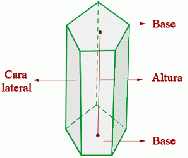
Prisma
Los prismas son poliedros que tienen dos caras paralelas e iguales llamadas bases y sus caras laterales son
paralelogramos.
Elementos de un prisma:
Altura de un prisma es la distancia entre las bases.
Los lados de las bases constituyen las aristas básicas y los lados de las caras laterales las aristas laterales, éstas son iguales y paralelas entre sí.
Volumen de un prisma: V= AB * h
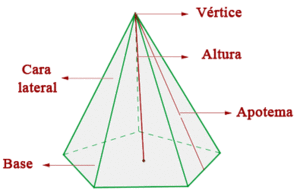
Pirámide
Una pirámide es un poliedro, cuya base es un polígono cualquiera y cuyas caras laterales son triángulos con un vértice
común, que es el vértice de la pirámide.
Elementos de una pirámide
La altura de la pirámide es el segmento perpendicular a la base, que une la base con el vértice.
Las aristas de la base se llaman aristas básicas y las aristas que concurren en el vértice, aristas laterales.
La apotema lateral de una pirámide regular es la altura de cualquiera de sus caras laterales.
Volumen de la piramide:
Poliedros regulares
Tetraedro
Un tetraedro regular es un poliedro regular formado por 4 triángulos equiláteros iguales. Es una pirámide triangular
regular.
Propiedades del tetraedro
Número de caras: 4.
Número de vértices: 4.
Número de aristas: 6.
Nº de aristas concurrentes en un vértice: 3.
Volumen del tetraedro:
Octaedro
Un octaedro es un poliedro regular formado por 8 triángulos equiláteros iguales.
Se puede considerar formado por la unión, desde sus bases, de dos pirámides cuadrangulares regulares iguales.
Propiedades del octaedro
Número de caras: 8.
Número de vértices: 6.
Número de aristas: 12.
Nº de aristas concurrentes en un vértice: 4.
Volumen del octaedro:
Cubo
Un cubo o hexaedro es un poliedro regular formado por 6 cuadrados iguales
Propiedades del cubo
Número de caras: 6.
Número de vértices: 8.
Número de aristas: 12.
Nº de aristas concurrentes en un vértice: 3.
Área del cubo:
Volumen del cubo:
Diagonal del cubo:
Dodecaedro
Un dodecaedro regular es un poliedro regular formado por 12 pentágonos regulares iguales.
Propiedades del dodecaedro
Número de caras: 12.
Número de vértices: 20.
Número de aristas: 30.
Nº de aristas concurrentes en un vértice: 3.
Volumen del dodecaedro
Icosaedro
Un icosaedro regular es un poliedro regular formado por 20 triángulos equiláteros iguales.
Propiedades del icosaedro
Número de caras: 20.
Número de vértices: 12.
Número de aristas: 30.
Nº de aristas concurrentes en un vértice: 5.
Volumen del icosaedro
Unidades de Medida
La unidad de medida de volumen en el Sistema Internacional de Unidades es el metro cúbico, aunque temporalmente también acepta el litro, que se utiliza comúnmente en la vida práctica.
Fuentes
(elipse) http://www.ditutor.com/geometria_analitica/elipses.html (elipse)