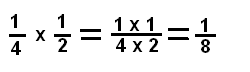Diferencia entre revisiones de «Multiplicación y división de fracciones comunes»
(Página creada con '{{desarrollo}} {{Definición |nombre=Multiplicación y división de fracciones comunes |imagen= |tamaño= |concepto= }} == Antecedentes == La teoría y el cálculo de las fracc...') |
|||
| Línea 1: | Línea 1: | ||
{{desarrollo}} | {{desarrollo}} | ||
{{Definición | {{Definición | ||
| − | |nombre=Multiplicación y división de fracciones comunes | + | |nombre=Multiplicación y división de fracciones comunes. |
|imagen= | |imagen= | ||
|tamaño= | |tamaño= | ||
| − | |concepto= | + | |concepto=El concepto matemático de fracción corresponde a la idea intuitiva de dividir una totalidad en partes iguales. Una fracción se representa matemáticamente por números que están escritos uno sobre otro y que se hallan separados por una línea recta horizontal llamada raya fraccionaria. |
| + | La fracción está formada por dos términos: el numerador y el denominador. El numerador está sobre la raya fraccionaria y el denominador es el que está bajo la raya fraccionaria. En general, en la fracción '''a / b''' (a sobre b). | ||
| + | |||
| + | '''a''' NUMERADOR: indica las partes que se toman. | ||
| + | '''b''' DENOMINADOR: indica las partes iguales en que se divide la unidad. | ||
| + | |||
}} | }} | ||
| Línea 11: | Línea 16: | ||
Gracias a los matemáticos indios , que revolucionaron el arte de calcular, podemos ahora expresar y calcular con [[fracciones]] de una forma más simple. | Gracias a los matemáticos indios , que revolucionaron el arte de calcular, podemos ahora expresar y calcular con [[fracciones]] de una forma más simple. | ||
| − | == Multiplicación y división de fracciones comunes == | + | == Multiplicación y división de fracciones comunes. == |
Al igual que los [[números naturales]], las fracciones se pueden multiplicar. | Al igual que los [[números naturales]], las fracciones se pueden multiplicar. | ||
Por ejemplo: | Por ejemplo: | ||
| Línea 17: | Línea 22: | ||
[[Archivo:imagen 1.PNG]] | [[Archivo:imagen 1.PNG]] | ||
| + | |||
| + | ¿Necesitas conocer cuántos botones representan ¾ (tres cuartas) partes de un conjunto de 8 botones? | ||
| + | |||
| + | [[Archivo:imagen 2.PNG]] | ||
| + | |||
| + | ¿Quieres saber qué parte del pastel se comió tu hermanita si le sirvieron ¼ (un cuarto) de la mitad del pastel? | ||
| + | |||
| + | [[Archivo:imagen 3.PNG]] | ||
| + | |||
| + | En los ejemplos anteriores has visto diferentes representaciones para la multiplicación de fracciones, en todos los casos el producto se calcula de la misma forma: | ||
| + | |||
| + | '''Observa que:''' | ||
| + | |||
| + | [[Archivo:imagen 4.PNG]] | ||
| + | |||
| + | [[Archivo:imagen 5.PNG]] | ||
| + | |||
| + | [[Archivo:imagen 6.PNG]] | ||
| + | |||
| + | En todos los casos se han multiplicado las fracciones multiplicando '''numerador por numerador y denominador por denominador.''' | ||
| + | |||
| + | '''Veamos otros ejemplos:''' | ||
| + | |||
| + | Halla el producto de las siguientes fracciones: | ||
| + | |||
| + | [[Archivo:imagen 7.PNG]] | ||
| + | |||
| + | ¿Cómo los resolvemos?: | ||
| + | |||
| + | [[Archivo:imagen 8.PNG]] | ||
| + | |||
| + | [[Archivo:imagen 9.PNG]] | ||
| + | |||
| + | [[Archivo:imagen 10.PNG]] | ||
| + | |||
| Línea 22: | Línea 62: | ||
http://www.ecured.cu/index.php?title=Fracciones&action=edit | http://www.ecured.cu/index.php?title=Fracciones&action=edit | ||
| + | |||
== Fuentes == | == Fuentes == | ||
*Libro de texto de Matemática 6to grado. Editorial Pueblo y Educación, edición 1990. | *Libro de texto de Matemática 6to grado. Editorial Pueblo y Educación, edición 1990. | ||
| − | + | *http://www.profesorenlinea.cl/matematica/FraccionConcepto.htm | |
Revisión del 17:05 21 abr 2011
| ||||
Antecedentes
La teoría y el cálculo de las fracciones como la utilizamos en la actualidad, se le atribuye al matemático hindú Brahmagupta (600 años a.n.e.) Gracias a los matemáticos indios , que revolucionaron el arte de calcular, podemos ahora expresar y calcular con fracciones de una forma más simple.
Multiplicación y división de fracciones comunes.
Al igual que los números naturales, las fracciones se pueden multiplicar. Por ejemplo: Si quieres saber el tiempo que inviertes en practicar la ortografía dedicando ¼ (un cuarto) de hora 3 veces a la semana, ¿cómo lo planteas?.
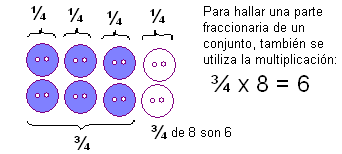
¿Necesitas conocer cuántos botones representan ¾ (tres cuartas) partes de un conjunto de 8 botones?
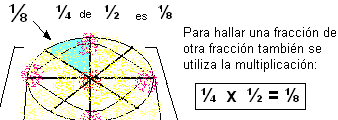
¿Quieres saber qué parte del pastel se comió tu hermanita si le sirvieron ¼ (un cuarto) de la mitad del pastel?
En los ejemplos anteriores has visto diferentes representaciones para la multiplicación de fracciones, en todos los casos el producto se calcula de la misma forma:
Observa que:
En todos los casos se han multiplicado las fracciones multiplicando numerador por numerador y denominador por denominador.
Veamos otros ejemplos:
Halla el producto de las siguientes fracciones:
¿Cómo los resolvemos?:
Referencias
http://www.ecured.cu/index.php?title=Fracciones&action=edit
Fuentes
- Libro de texto de Matemática 6to grado. Editorial Pueblo y Educación, edición 1990.
- http://www.profesorenlinea.cl/matematica/FraccionConcepto.htm