Diferencia entre revisiones de «Fórmulas de derivadas»
| Línea 1: | Línea 1: | ||
| − | {{Objeto|nombre= Tabla de derivadas |imagen=Dportada.jpg |descripcion= }} '''Derivada de una función.''' Históricamente el concepto de derivada es debido a Newton y a Leibnitz. Sus definiciones surgen a raíz del concepto de | + | {{Objeto|nombre= Tabla de derivadas |imagen=Dportada.jpg |descripcion= }} '''Derivada de una función.''' Históricamente el concepto de derivada es debido a[[Isacc_Newton|Newton]] y a [[Leibnitz|Leibnitz]]. Sus definiciones surgen a raíz del concepto de [[Límite_de_una_función|límite]]. |
== Algunos conceptos<br> == | == Algunos conceptos<br> == | ||
| − | Los comunes son los siguientes:<br> | + | Los más comunes son los siguientes:<br> |
| − | -Pendiente de una curva. | + | -Pendiente de una curva.<br> |
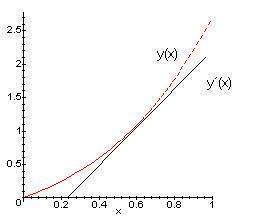
| − | + | - Tangente a una curva. La recta tangente al grafico de la función f en el punto. P = (x , f(x) ) es la recta que pasa por[[Image:Defini1.jpg|thumb|right]] P con pendiente igual a la derivada de f en x. | |
| − | |||
| − | - Tangente a una curva. La recta tangente al grafico de la función f en el punto. P = (x , f(x) ) es la recta que pasa por P con pendiente igual a la derivada de f en x. | ||
| − | |||
| − | |||
- Velocidad de una partícula que se mueve sobre una línea recta. La velocidad en el instante t de un objeto, cuya posición sobre una recta viene dada por f(t) en el instante t, es la derivada de f en el punto t. El valor absoluto de la velocidad es el módulo de esa cantidad. | - Velocidad de una partícula que se mueve sobre una línea recta. La velocidad en el instante t de un objeto, cuya posición sobre una recta viene dada por f(t) en el instante t, es la derivada de f en el punto t. El valor absoluto de la velocidad es el módulo de esa cantidad. | ||
| − | |||
| − | |||
- Amplificación de una proyección entre rectas. La amplificación en x de una lente que proyecta el punto x de una recta sobre el punto f(x) de otra recta es la derivada de f en x. | - Amplificación de una proyección entre rectas. La amplificación en x de una lente que proyecta el punto x de una recta sobre el punto f(x) de otra recta es la derivada de f en x. | ||
Revisión del 09:30 26 abr 2011
| ||||
Derivada de una función. Históricamente el concepto de derivada es debido aNewton y a Leibnitz. Sus definiciones surgen a raíz del concepto de límite.
Algunos conceptos
Los más comunes son los siguientes:
-Pendiente de una curva.
- Tangente a una curva. La recta tangente al grafico de la función f en el punto. P = (x , f(x) ) es la recta que pasa por
P con pendiente igual a la derivada de f en x.
- Velocidad de una partícula que se mueve sobre una línea recta. La velocidad en el instante t de un objeto, cuya posición sobre una recta viene dada por f(t) en el instante t, es la derivada de f en el punto t. El valor absoluto de la velocidad es el módulo de esa cantidad.
- Amplificación de una proyección entre rectas. La amplificación en x de una lente que proyecta el punto x de una recta sobre el punto f(x) de otra recta es la derivada de f en x.
- Densidad de un material. La densidad de x de un material distribuido a lo largo de una recta de forma tal que los x centímetros de la izquierda tengan una masa de f(x) gramos es igual a la derivada de f en x.
Fórmulas de derivadas
Derivada de una constante
Derivada de x
Derivada de función afín
Derivada de una potencia
Derivada de una raíz cuadrada
Derivada de una raíz
Derivada de suma
Derivada de una constante por una función
Derivada de un producto
Derivada de constante partida por una función
Derivada de un cociente
Derivada de la función exponencial
Derivada de la función exponencial de base e
Derivada de un logaritmo
Derivada de un logaritmo neperiano
Derivada de la función seno
Derivada de la función coseno
Derivada de la función tangente
Derivada de la función cotangente
Derivada de la secante
Derivada de la cosecante
Derivada de la función arcoseno
Derivada de la función arcocoseno
Derivada de la función arcotangente
Derivada de la función arcocotangente
Derivada de la función arcosecante
Derivada de la función arcocosecante
Derivada del arcocosecante la función potencial-exponencial
Regla de la cadena
Fórmula de derivada implícita
