Diferencia entre revisiones de «Ángulos en la circunferencia»
| Línea 26: | Línea 26: | ||
Véase también que, en una misma circunferencia, o en circunferencias iguales, a '''ángulos centrales iguales''' corresponden arcos y'''cuerdas''' iguales y, a mayor cuerda corresponde mayor arco y viceversa. | Véase también que, en una misma circunferencia, o en circunferencias iguales, a '''ángulos centrales iguales''' corresponden arcos y'''cuerdas''' iguales y, a mayor cuerda corresponde mayor arco y viceversa. | ||
== Ángulo inscrito en una circunferencia == | == Ángulo inscrito en una circunferencia == | ||
| + | |||
| + | Un ángulo cuyo vértice pertenece a una circunferencia y sus lados la intersecan además en otros dos puntos se denomina '''ángulo inscrito''' en la [[circunferencia]]. | ||
| + | [[Archivo:Inscrito.PNG]] | ||
| + | La demostración de lo planteado en la figura puede verse en: | ||
| + | [*http://apuntes-dematematicas.blogspot.com/2009/03/circunferencias.html] | ||
=== Relación entre ángulos inscritos === | === Relación entre ángulos inscritos === | ||
Revisión del 13:33 23 jun 2011
| ||||||
Ángulos en la circunferencia. En la enseñanza de la Matemática se deben utilizar los conceptos y teoremas fundamentales de forma estructurada, lo que para la enseñanza de la Geometría tiene sus particularidades. En este tema se habla de los ángulos en relación con las circunferencias. Se definen los conceptos de ángulo central, inscrito, semi-inscrito, interior y exterior y se muestran algunos resultados geométricos importantes que utilizan estos conceptos.
Sumario
Aplicaciones
En la enseñanza de la Geometría se comprenden de forma fragmentada los conceptos y teoremas, y su utilización en la resolución de problemas es muy limitada. La Geometría está encaminada a prepararse para resolver problemas geométricos de construcción, de cálculo y de demostración a partir de las relaciones de igualdad de triángulos, en la circunferencia y la semejanza. El tratamiento de estos conceptos en la solución de problemas de este tipo, posibilita la formación de una visión global inicial de las habilidades matemáticas para calcular longitudes de segmentos, arcos y amplitudes de ángulos en situaciones dadas.
Ángulo central
Los lados del ángulo central son radios de la circunferencia por lo que OA = OB. La amplitud de un arco es igual a la amplitud de su ángulo central correspondiente.
Relación entre ángulos centrales
Observemos que, en una misma circunferencia, o en circunferencias iguales, a ángulos centrales iguales corresponden arcos iguales.
Véase también que, en una misma circunferencia, o en circunferencias iguales, a ángulos centrales iguales corresponden arcos ycuerdas iguales y, a mayor cuerda corresponde mayor arco y viceversa.
Ángulo inscrito en una circunferencia
Un ángulo cuyo vértice pertenece a una circunferencia y sus lados la intersecan además en otros dos puntos se denomina ángulo inscrito en la circunferencia.
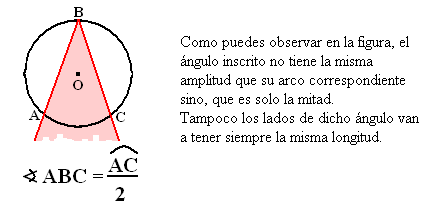
La demostración de lo planteado en la figura puede verse en: [*http://apuntes-dematematicas.blogspot.com/2009/03/circunferencias.html]
Relación entre ángulos inscritos
Véase también
Fuente
- Libro de texto de Matemática 8vo grado. Editorial Pueblo y Educación, 1990.