Diferencia entre revisiones de «Conjunto Numérico»
| Línea 1: | Línea 1: | ||
| − | {{ | + | {{Objeto|nombre=Conjunto Numérico|imagen=Conjuntos_Numéricos.JPG|descripcion=}}'''Conjunto Numérico.''' Desde sus inicios el hombre tomó conciencia del uso de la palabra conjunto al formar grupos de animales, grupos de herramientas o simplemente al ellos unirse en grupos por diferentes intereses. Según el [[Diccionario de la Real Academia de la Lengua Española]] conjunto es “totalidad de los entes matemáticos que tienen una propiedad común” en otras palabras conjunto no es más que una colección de objetos que tienen una o más características o propiedades en común. |
| − | '''Notación''' | + | == '''Notación''' == |
Existen pautas a tener en cuanta a la hora de expresar los conjuntos: | Existen pautas a tener en cuanta a la hora de expresar los conjuntos: | ||
| − | + | *Los conjuntos se denotan con letras mayúsculas.<br> | |
| + | *Los elementos que forman los conjuntos se encierran entre llaves. ·Los elementos se denotan con letras minúsculas. <br> | ||
| + | *Para expresar con elemento pertenece a un conjunto se usa el siguiente símbolo [[Image:Pertenece.JPG]] así como para representar que no pertenece el siguiente [[Image:Nopertenece.JPG]].<br> | ||
| + | *Un conjunto vacío se representa de la siguiente manera {}=[[Image:Vacio.JPG]].<br> | ||
| + | *El subconjunto propio se representa de esta manera [[Image:Subconjunto propio.JPG]], subconjunto [[Image:Subconjunto1.JPG]], no es subconjunto [[Image:No es subconjunto.JPG]], menor < y mayor >. | ||
| − | '''Pertenencia''' | + | == '''Pertenencia''' == |
| − | Si A es un conjunto y x es elemento de ese conjunto, se puede decir que x pertenece al conjunto A y se expresa de la siguiente manera: x | + | Si A es un conjunto y x es elemento de ese conjunto, se puede decir que x pertenece al conjunto A y se expresa de la siguiente manera: x [[Image:Pertenece.JPG]] A. De no pertenecer entonces lo escribimos de esta manera x [[Image:Nopertenece.JPG]] A. |
| − | '''Cardinalidad''' | + | == '''Cardinalidad''' == |
| − | La cardinalidad es determinada por la cantidad de elementos que contenga un conjunto. Por ejemplo A = {a,b,c,d} se puede decir que su cardinalidad es 4 y se expresa de la siguiente manera | + | La cardinalidad es determinada por la cantidad de elementos que contenga un conjunto. Por ejemplo A = {a,b,c,d} se puede decir que su cardinalidad es 4 y se expresa de la siguiente manera [[Image:Cardinalidad.JPG]](A) = 4. |
| − | '''Equivalencia entre conjuntos.''' | + | == '''Equivalencia entre conjuntos.''' == |
Se dice que dos conjuntos son equivalentes si tienen el mismo número de elementos y se puede establecer entre ellos una correspondencia de uno a uno, un ejemplo de esto es: A = {perro, gato, jirafa} y A = {2,3,4}. | Se dice que dos conjuntos son equivalentes si tienen el mismo número de elementos y se puede establecer entre ellos una correspondencia de uno a uno, un ejemplo de esto es: A = {perro, gato, jirafa} y A = {2,3,4}. | ||
| − | <br> '''Igualdad entre conjuntos.''' | + | == <br> '''Igualdad entre conjuntos.''' == |
Dos conjuntos son iguales si y solo si tienen los mismos elementos sin importar el orden de estos ni la cantidad. | Dos conjuntos son iguales si y solo si tienen los mismos elementos sin importar el orden de estos ni la cantidad. | ||
| − | <br> '''Clases de Conjuntos.''' | + | == <br> '''Clases de Conjuntos.''' == |
| − | + | *Conjunto Unitario: Es aquel que está formado por un solo elemento. | |
| − | + | *Conjunto Finito: Es aquel conjunto en el cual los elementos se pueden definir del primero al último. | |
| − | + | *Conjunto Infinito: Es cuando a un conjunto no se les puede contar todos y cada uno de los elementos. | |
| + | *Conjunto Vacío: Es aquel que carece de elementos.<br> | ||
| + | *Subconjunto: A es subconjunto de B si y solo si cada elemento de A está contenido en B. | ||
| + | *Conjunto Universo: Es el que contiene en sí todos los elementos del tema de estudio. | ||
<br> | <br> | ||
| − | '''Operaciones entre conjuntos''' | + | == '''Operaciones entre conjuntos''' == |
Entre los conjuntos se pueden desarrollar varias operaciones para lograr nuevas combinaciones entre ellos. Estas operaciones son muy parecidas a las que se ejecutan entre los números corrientes. A continuación se definen las principales: | Entre los conjuntos se pueden desarrollar varias operaciones para lograr nuevas combinaciones entre ellos. Estas operaciones son muy parecidas a las que se ejecutan entre los números corrientes. A continuación se definen las principales: | ||
| − | + | === '''Unión''' === | |
| − | |||
| − | |||
| − | [[Image: | + | [[Image:Union1.JPG|thumb|141x112px|A[[Image:Union_conjun.JPG]]B Unión.]] Se define como unión de dos conjuntos al conjunto compuesto por todos los elementos que están en ambos. Se denota por AÈB. Donde A[[Image:Union conjun.JPG]]B={x; x[[Image:Pertenece.JPG]]A o x[[Image:Pertenece.JPG]]B}. |
| − | + | === '''Intersección''' === | |
| − | Se define como intersección a los elementos comunes entre dos conjuntos. Entre los conjuntos A y B serían los elementos que están en A pero que también están en B y se denota | + | [[Image:Interseccion.JPG|thumb|148x122px|A[[Image:Inter_conjunto.JPG]]B Intersección.]] Se define como intersección a los elementos comunes entre dos conjuntos. Entre los conjuntos A y B serían los elementos que están en A pero que también están en B y se denota A[[Image:Inter conjunto.JPG]]B = {x; x[[Image:Pertenece.JPG]]A y x[[Image:Pertenece.JPG]]B}. |
| − | Cuando dos conjuntos no tienen elementos comunes se les llama conjuntos disjuntos y su intersección es el conjunto vacío. | + | Cuando dos conjuntos no tienen elementos comunes se les llama conjuntos disjuntos y su intersección es el conjunto vacío. |
| − | '''Diferencia''' | + | === '''Diferencia''' === |
Se define como diferencia de dos conjuntos a los elementos que están en uno que no están en el otro y se evidencia en el siguiente ejemplo: | Se define como diferencia de dos conjuntos a los elementos que están en uno que no están en el otro y se evidencia en el siguiente ejemplo: | ||
| Línea 55: | Línea 60: | ||
A-B = {1,2} | A-B = {1,2} | ||
| − | B-A = {6} | + | B-A = {6} |
| − | <br> | + | [[Image:Diferencia1.JPG|188x160px]][[Image:Diferencia2.JPG|191x157px]]<br> |
| − | '''Complemento de un Conjunto.''' | + | == '''Complemento de un Conjunto.''' == |
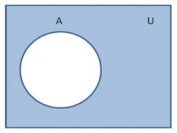
Se define como complemento de un conjunto a los elementos del universo que no pertenecen a dicho conjunto. Se define de la siguiente manera: | Se define como complemento de un conjunto a los elementos del universo que no pertenecen a dicho conjunto. Se define de la siguiente manera: | ||
| − | A´= {x; | + | A´= {x; x[[Image:Pertenece.JPG]]U y x[[Image:Pertenece.JPG]]A} donde U es el conjunto universo. |
| − | |||
| − | |||
| − | <br> | + | [[Image:Universo.JPG|177x133px]]<br> |
| − | + | == Bibliografía<br> == | |
| − | <br> | + | *Lugo, Shneidr (1969). Teoría de Conjuntos y Dominios Numéricos.<br> |
| + | *List, G. (1977). Lógica [[Matemática]], Teoría de Conjuntos y Dominios Numéricos.<br> | ||
| + | *Brehmr, S. (1976). Analisis Matemático I.<br> | ||
<br> | <br> | ||
| − | <br> | + | == Referencia<br> == |
| − | <br> | + | *[http://drae.rae.es/ Diccionario de la Real Academia de la Lengua Española.]<br> |
<br> | <br> | ||
Revisión del 16:37 24 jun 2010
| ||||
Conjunto Numérico. Desde sus inicios el hombre tomó conciencia del uso de la palabra conjunto al formar grupos de animales, grupos de herramientas o simplemente al ellos unirse en grupos por diferentes intereses. Según el Diccionario de la Real Academia de la Lengua Española conjunto es “totalidad de los entes matemáticos que tienen una propiedad común” en otras palabras conjunto no es más que una colección de objetos que tienen una o más características o propiedades en común.
Sumario
Notación
Existen pautas a tener en cuanta a la hora de expresar los conjuntos:
- Los conjuntos se denotan con letras mayúsculas.
- Los elementos que forman los conjuntos se encierran entre llaves. ·Los elementos se denotan con letras minúsculas.
- Para expresar con elemento pertenece a un conjunto se usa el siguiente símbolo Archivo:Pertenece.JPG así como para representar que no pertenece el siguiente Archivo:Nopertenece.JPG.
- Un conjunto vacío se representa de la siguiente manera {}=Archivo:Vacio.JPG.
- El subconjunto propio se representa de esta manera Archivo:Subconjunto propio.JPG, subconjunto Archivo:Subconjunto1.JPG, no es subconjunto Archivo:No es subconjunto.JPG, menor < y mayor >.
Pertenencia
Si A es un conjunto y x es elemento de ese conjunto, se puede decir que x pertenece al conjunto A y se expresa de la siguiente manera: x Archivo:Pertenece.JPG A. De no pertenecer entonces lo escribimos de esta manera x Archivo:Nopertenece.JPG A.
Cardinalidad
La cardinalidad es determinada por la cantidad de elementos que contenga un conjunto. Por ejemplo A = {a,b,c,d} se puede decir que su cardinalidad es 4 y se expresa de la siguiente manera Archivo:Cardinalidad.JPG(A) = 4.
Equivalencia entre conjuntos.
Se dice que dos conjuntos son equivalentes si tienen el mismo número de elementos y se puede establecer entre ellos una correspondencia de uno a uno, un ejemplo de esto es: A = {perro, gato, jirafa} y A = {2,3,4}.
Igualdad entre conjuntos.
Dos conjuntos son iguales si y solo si tienen los mismos elementos sin importar el orden de estos ni la cantidad.
Clases de Conjuntos.
- Conjunto Unitario: Es aquel que está formado por un solo elemento.
- Conjunto Finito: Es aquel conjunto en el cual los elementos se pueden definir del primero al último.
- Conjunto Infinito: Es cuando a un conjunto no se les puede contar todos y cada uno de los elementos.
- Conjunto Vacío: Es aquel que carece de elementos.
- Subconjunto: A es subconjunto de B si y solo si cada elemento de A está contenido en B.
- Conjunto Universo: Es el que contiene en sí todos los elementos del tema de estudio.
Operaciones entre conjuntos
Entre los conjuntos se pueden desarrollar varias operaciones para lograr nuevas combinaciones entre ellos. Estas operaciones son muy parecidas a las que se ejecutan entre los números corrientes. A continuación se definen las principales:
Unión

Se define como unión de dos conjuntos al conjunto compuesto por todos los elementos que están en ambos. Se denota por AÈB. Donde AArchivo:Union conjun.JPGB={x; xArchivo:Pertenece.JPGA o xArchivo:Pertenece.JPGB}.
Intersección
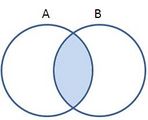
Se define como intersección a los elementos comunes entre dos conjuntos. Entre los conjuntos A y B serían los elementos que están en A pero que también están en B y se denota AArchivo:Inter conjunto.JPGB = {x; xArchivo:Pertenece.JPGA y xArchivo:Pertenece.JPGB}.
Cuando dos conjuntos no tienen elementos comunes se les llama conjuntos disjuntos y su intersección es el conjunto vacío.
Diferencia
Se define como diferencia de dos conjuntos a los elementos que están en uno que no están en el otro y se evidencia en el siguiente ejemplo:
Sean A={1,2,3,4,5} y B={3,4,5,6}
A-B = {1,2}
B-A = {6}
Complemento de un Conjunto.
Se define como complemento de un conjunto a los elementos del universo que no pertenecen a dicho conjunto. Se define de la siguiente manera:
A´= {x; xArchivo:Pertenece.JPGU y xArchivo:Pertenece.JPGA} donde U es el conjunto universo.
Bibliografía
- Lugo, Shneidr (1969). Teoría de Conjuntos y Dominios Numéricos.
- List, G. (1977). Lógica Matemática, Teoría de Conjuntos y Dominios Numéricos.
- Brehmr, S. (1976). Analisis Matemático I.
Referencia